Prédire le prix du Bitcoin ? Le pari risqué du modèle Stock-to-Flow (S2F)

22 mars 2019. L’internaute anonyme PlanB, également connu sous son identifiant Twitter @100trillionUSD, publie sur Medium un papier au titre aussi énigmatique qu’évocateur : « Modeling Bitcoin’s Value with Scarcity ». Cette étude connaîtra un retentissement certain au sein de la cryptosphère, voire en dehors. PlanB y dévoile un modèle statistique de sa conception, basé sur la notion de Stock-to-Flow, et visant à modéliser la valeur de marché du bitcoin. Outre le mécanisme intéressant proposé par PlanB pour expliquer la relation entre la rareté et la valeur du bitcoin, ce qui frappe les esprits, ce sont les conclusions : un bitcoin s’échangeant à 55 000 dollars l’unité quelques mois après le halving de mai 2020. Un pari… risqué ?

Dans une série de 2 articles, nous commencerons par rappeler ce en quoi consiste un modèle statistique et comment on peut en évaluer la pertinence. Puis, nous nous pencherons sur le modèle Stock-to-Flow de PlanB, son contexte, ce qu’il indique et comment l’analyser.

Modèle statistique : quèsaco?

En sciences, le terme de modèle renvoie directement à la notion de « modélisation », c’est-à-dire chercher à représenter un phénomène complexe de manière simplifiée, pour en saisir l’essentiel et tenter de l’expliquer par un certain mécanisme. Ainsi, un modèle est par définition une approximation de la réalité, qui ignore volontairement (et consciemment) certains aspects, soit parce que jugés de faible importance dans le phénomène en général, soit parce qu’on a décidé de ne pas les mesurer pour d’autres raisons (notamment parce qu’il est en pratique impossible de tout mesurer. On va alors, soit fixer les paramètres à ne pas étudier, soit, au contraire, les laisser libres et faire de la randomisation. On prend alors l’hypothèse que ces aspects peuvent être mis de côté. Quoi qu’il en soit, il est indispensable d’avoir conscience de cette hypothèse pour pouvoir la questionner et la mettre en regard des résultats que l’on obtient à l’issue de la modélisation.

Dans le cas précis d’un modèle statistique ayant pour objectif final d’émettre des prédictions, l’idée est de supposer que parmi l’ensemble des paramètres influant sur un phénomène donné, on peut en isoler un (ou quelques-uns) qui a une influence prépondérante et qui permet donc, à lui seul, d’expliquer une bonne partie du phénomène. On considère alors les autres paramètres comme négligeables, et on ne les intègre pas dans la suite du modèle.

Imaginons, par exemple, une île où on cultive des fruits exotiques : les gloups. Un des agriculteurs cherche à modéliser la vitesse de croissance des gloups afin d’optimiser l’environnement de sa plantation, ce qui améliorera les rendements. Bien entendu, tout un tas de facteurs entre en jeu : la température, la pluviométrie, le vent, les animaux, les polluants, etc. Il décide cependant de ne considérer que l’hydrométrie, considérant les autres comme négligeables. C’est là une hypothèse qu’il faut bien garder à l’esprit, pour en évaluer plus tard la pertinence.

Maintenant qu’il a fait quelques simplifications, notre cultivateur peut s’atteler à la tâche cruciale de la collecte des données. Il va donc, dans le cadre de son modèle, s’intéresser à 2 grandeurs physiques : la pluviométrie, qu’il mesure chaque jour en millimètres de précipitations, et la croissance de ses fruits, dont il mesure le diamètre quotidiennement.

En transposant ses mesures sur un graphique, où il place en abscisse  les précipitations et en ordonnées la croissance des fruits, il obtient quelque chose d’intéressant : plus il pleut, plus les fruits semblent grossir vite.

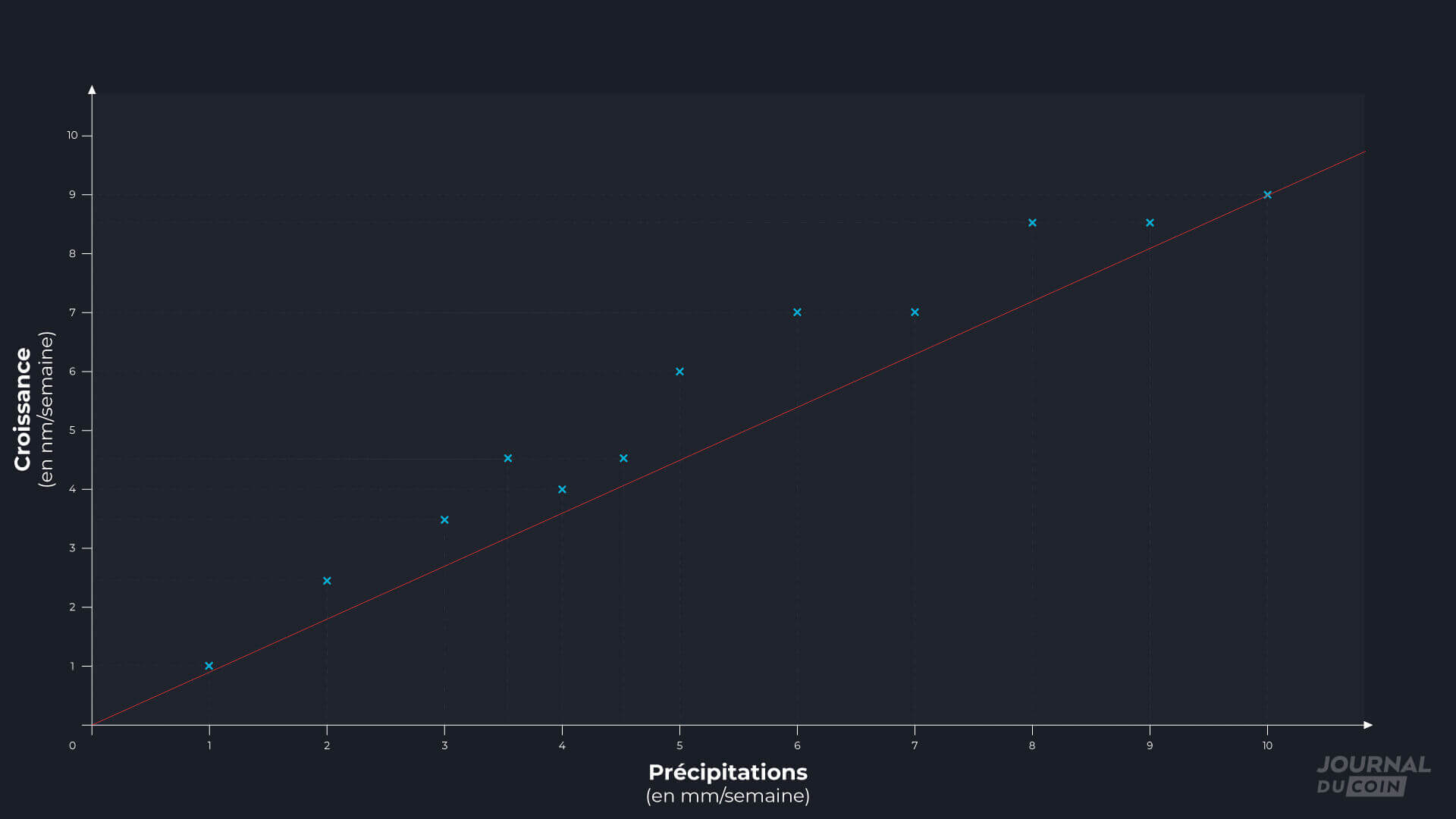
Notre cultivateur remarque même que les différents points correspondant aux données qu’il a collectées semblent s’aligner sur une même ligne droite. Il en déduit un modèle dans lequel la croissance des gloups est liée à la pluviométrie par une équation linéaire de la forme :

croissance = a * pluviométrie + b

Cette équation correspond à la ligne droite qu’il trace sur le même graphe et qui s’ajuste le mieux aux points expérimentaux. On parle, pour cette courbe, de régression linéaire. Le nombre a correspond à la pente de la courbe : le nombre de millimètres supplémentaires que gagnent en une semaine les gloups, lorsque les précipitations hebdomadaires augmentent d’un millimètre. Le nombre b correspond, quant à lui, à la croissance des gloups lorsqu’il ne pleut pas et, dans ce cas précis, est égal à 0.

Notre cultivateur de gloups est donc parti d’une hypothèse initiale (« la croissance des Gloups est très influencée par la pluie »), qui semble confirmée par l’allure du graphe qu’il obtient en compilant les données expérimentales. S’il semble donc qu’il y ait bien une corrélation entre la pluviométrie et la croissance des fruits, encore faut-il évaluer la qualité de la régression linéaire.

Comment évaluer la pertinence d’un modèle statistique ?

Pour évaluer la qualité d’un modèle statistique, il existe un grand nombre d’outils. Nous nous contenterons d’en aborder ici 2 principaux, car ils nous seront également utiles dans notre prochain article, où nous aborderons plus précisément le modèle Stock-to-Flow.

Le coefficient R2

Le coefficient R2 caractérise une régression linéaire et indique à quel point la prédiction du modèle colle avec les données. Le R2 est compris entre 0 et 1. Plus il est proche 1, plus les écarts entre la régression et les données sont faibles. Les mesures n’étant jamais parfaites, et le monde ne se comportant de toute façon jamais tout à fait comme le prédisent les modèles, le coefficient R2 n’est jamais égal à 1. On définit alors, de manière plus ou moins explicite, un seuil à partir duquel le R2 est suffisamment grand pour que le modèle puisse être considéré comme satisfaisant. Il n’y a pas vraiment de règle établie sur une valeur seuil du R2. Toutefois, on sera, par exemple, beaucoup plus exigeant en physique qu’en économie.

Dans l’exemple de nos fruits tropicaux, on obtient un coefficient R2 égal à 0,98, ce qui est tout à fait satisfaisant et permet de conclure qu’il y a effectivement corrélation entre la pluviométrie et la croissance des gloups.

La valeur p

La valeur p, appelée p-value en anglais, correspond à la probabilité que l’association observée entre 2 grandeurs (ici, la pluviométrie et la croissance des Glubs) soit due au hasard, non à une vraie relation, un réel effet. Plus la valeur p est faible, plus on peut estimer que les observations (les données) traduisent un réel effet (l’effet de la pluie sur la croissance des gloups).

La valeur p est aujourd’hui, et depuis quelques années, au centre de débats passionnés dans la sphère scientifique, concernant notamment son emploi parfois maladroit dans certaines publications. Elle reste cependant très pertinente et abondamment utilisée.

Un modèle bâti à partir d’observations

S’il y a une chose qu’il faut également bien comprendre, et qui aura son importance dans notre second article, c’est que le modèle de notre cultivateur se base sur des observations et sans contrôle strict de l’ensemble des paramètres. Ce n’est donc pas à strictement parler une démonstration de l’influence de la pluie sur la croissance des gloups, mais il s’agit d’une suggestion. En effet, on ne peut pas exclure qu’un autre facteur sous-jacent influence à la fois la pluie et la croissance des fruits et qu’il n’y ait pas de lien entre la pluie et la taille des fruits. Autrement dit, corrélation n’est pas causalité.

Il n’en reste pas moins qu’une corrélation suggère une causalité et que, s’il existe en plus un mécanisme solide à même d’expliquer une causalité entre les deux grandeurs, cette suggestion s’en trouve renforcée.

Enfin, il ne faut pas perdre de vue que certains paramètres que l’on a sciemment écartés lors de la construction du modèle pourraient voir leur influence augmenter pour certaines raisons. Une maladie causant une réduction de la taille des fruits et qui, jusqu’à maintenant, ne touchait que peu de fruits, pourrait se répandre, et le modèle perdrait alors sa valeur prédictive.

Dans cet article introductif, nous avons passé en revue les concepts de base sous-jacents à la notion de modèle statistique. Nous avons vu comment ces derniers sont construits, comment les évaluer et quelles déductions on peut en tirer. Tout ceci nous servira de base pour étudier, dans un second article, le modèle Stock-to-Flow proposé par PlanB.