
Satoshi Nakamoto a-t-il programmé la mort de Bitcoin ? – Chapitre IV : « Complexité Algorithmique et P = NP »
Avertissement : cet article (ainsi que les 3 chapitres qui le précède) constitue une œuvre de fiction, prétexte à la présentation des principes mathématiques et cryptographiques permettant à Bitcoin de fonctionner.
31 Février 2023, 20h55 UTC-5 — Le monde est sous le choc. Le bitcoin s’est effondré lors de la session asiatique, son prix ? Vous ne voulez pas le savoir. Les mauvaises nouvelles ne font que s’enchaîner les unes après les autres. Ce n’est plus « Bitcoin est mort » que l’on lit dans les journaux en ce jour, mais bien « Internet est mort ». La panique est telle que plus personne ne tente même de comprendre ce qu’il s’est passé, mais essaye plutôt de sauver ce qui peut l’être. Une rumeur commence à émerger, Satoshi serait de retour et il va s’exprimer aujourd’hui. La quasi-totalité du globe est connectée sur la diffusion orchestrée par le bureau ovale.
La conférence commence. Un homme affaibli tenant à peine debout se présente, des engelures plein les doigts et le visage meurtri par le froid.
« Je suis celui que l’on appelle communément Satoshi Nakamoto, et que vous me croyiez n’as plus aucune importance désormais. Alors qu’on m’en attribuait les faits, ce n’est pas moi qui ai vidé mon portefeuille contenant un million de Bitcoin. Il y a de cela 14 ans, j’ai construit ce wallet soigneusement dans un but précis, bien qu’à l’époque, je ne pensais pas ça possible. Ce dernier devait servir à pousser la recherche sur la seule faille qui pouvait atteindre Bitcoin, le problème P = NP, en agissant comme un incitatif conséquent. L’attaquant a trouvé un moyen d’inverser ma clé publique, certainement en dérivant la résolution d’un problème NP-complet. Hier, ce n’est pas seulement ma création qui est tombée, mais toute la cryptographie moderne. Mesdames, Messieurs, les socles les plus fondamentaux de notre société technologique sont révolus. Internet n’est plus sûr, et l’économie va probablement s’effondrer. Aujourd’hui, j’ai peur pour le destin de l’huma….»
Table des matières
Voici venu le temps de l’apocalypse, et de la réponse à l’introduction faite lors du démarrage de cette série et à votre curiosité qui, je l’espère, n’a fait que grandir lors de ces publications.
Car malgré une date du 30 février constituant une pure invention de l’esprit, et un sujet aguicheur permettant de réintroduire les fondamentaux de la cryptographie, cette petite fiction n’est ni dénuée de sens, ni totalement fantaisiste. Mais j’en suis sûr, vous trouverez que le chemin en valait la chandelle. Comme l’adage le dit, ce n’est pas la destination qui compte, mais bien le voyage non ?
Satoshi Nakamoto, en posant une question fondamentale sur les limites algorithmiques de nos connaissances, a-t-il planifié une fin pour Bitcoin ?
La complexité algorithmique
Mesurer la performance d’un algorithme
Lors des trois derniers articles, nous avons essayé de comprendre quels étaient les remparts mathématiques protégeant aussi bien nos clés privées, que la construction de la chaîne de block en elle-même via le mining. Ce long voyage ayant pour but de vous introduire au concept de la complexité algorithmique.
La complexité algorithmique est la mesure de la performance d’un algorithme à réaliser un problème mathématique. Pour la quantifier, nous dénombrons les opérations élémentaires nécessaires à cette résolution.
Prenons l’exemple d’un algorithme cherchant le plus petit nombre dans une liste de 10 nombres. La manière la plus simple et intuitive de réaliser ce problème est de suivre cet algorithme :
- Lire le nombre,
- Le comparer au nombre suivant,
- Garder le chiffre le plus petit en mémoire
- Répéter cette opération jusqu’à la fin de la liste.
Lorsque vous avez comparé tous les nombres, vous êtes sûr d’avoir trouvé le nombre le plus petit. Pour résoudre ce problème avec 10 nombres, nous devons réaliser 10 opérations. Si nous généralisons, pour une liste à N nombres, N opérations sont nécessaires.
À présent, complexifions le problème. Il ne faut plus seulement chercher le plus petit nombre de la liste, mais les classer dans l’ordre croissant. L’algorithme précèdent nous permet de le faire en trouvant le plus petit nombre que l’on transfère dans une nouvelle liste. Il suffit de relancer l’algorithme autant de fois qu’il y a de nombre à classer.
Pour classer 10 nombres, une cinquantaine d’opérations sont nécessaire. Si nous généralisons, pour N nombres, environ N^2/2 opérations doivent être éxécutés. Dès lors il devient intéressant de se pencher sur l’évolution du nombre d’opération nécessaire en fonction du nombre de donnée à traiter.

Pour ces deux exemples, lorsqu’on multiplie par 10 le nombre de données de la liste, nous multiplions aussi par 10 le nombre d’opérations pour le premier algorithme. En revanche pour le second, le nombre d’opérations est multiplié par 100 ! La complexité de notre premier algorithme est linéaire, alors qu’elle est quadratique (ou polynomiale) pour le second.
Mais cet algorithme de tri est un peu naïf, il est possible de réduire ce nombre d’opérations. Aujourd’hui, l’algorithme le plus efficace nécessite une trentaine d’opérations pour dix nombres, avec une complexité dites linéarithmique.
Classement de la complexité
Il devient donc possible de classer les algorithmes en fonction de leur complexité. On considère comme « difficile » tout algorithme de complexité supérieur à polynomiale. Seul les problèmes pour lesquelles nous n’avons pas trouvé de résolution de type polynomiale sont acceptables pour des systèmes cryptographique.
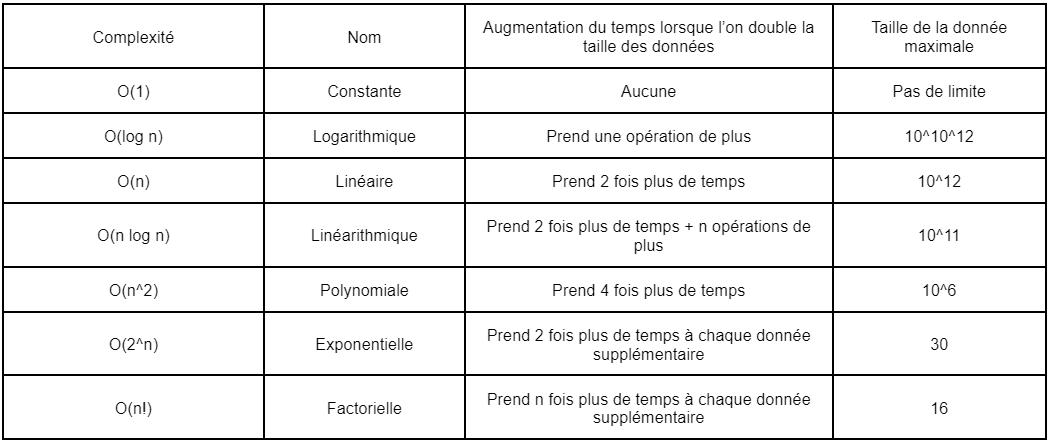
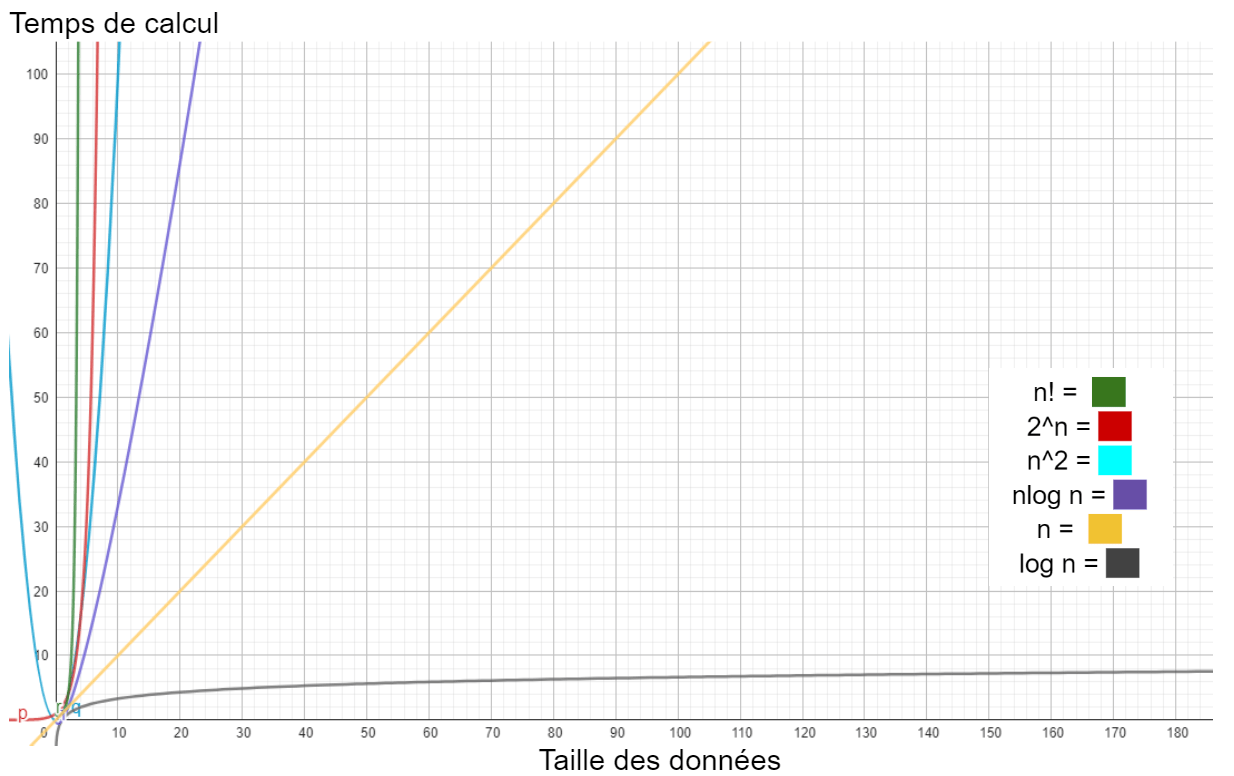
Par exemple, le problème du logarithme discret protégeant l’irréversibilité de nos clés publiques possède une complexité exponentielle. Il en découle des temps de résolution déraisonnablement long, en tout cas pour les algorithmes connus.
Dans certain cas, les mathématiciens sont en mesure de prouver que pour un problème donnée, la complexité ne peut être réduite sous un certain seuil. En extrapolant l’optimisation de nos algorithmes, une nouvelle question se pose. Jusqu’à quel point pouvons-nous la réduire pour l’ensemble des problèmes existant ? Est-il possible de la réduire de sorte à ce que tous soient résolubles en un temps polynomial et donc relativement “facilement” ?
Un des 7 problèmes du millénaire : P = NP
Extrapolation de la réduction de la complexité
Après des centaines de lignes et des milliers de mots, nous voici arrivés à un des septs Graal des mathématiques. P = NP est un des plus prestigieux problèmes des mathématiques, posé par l’institut Clay en 2000. Il est au cœur des limites algorithmiques du savoir. Dans sa forme la plus simple, il revient à poser la question :
Est-ce que chercher est plus dur que vérifier ?
Voici ici toute la question que j’ai essayé subtilement de révéler au cours de mes précédents articles en démontrant que les verrous mathématiques de la cryptographie sont extrêmement complexes à résoudre, mais en revanche, leur solution très facile à vérifier. C’est ce que l’on appelle l’asymétrie computationnelle. Les fondements de la cryptographie et de Bitcoin n’ont de sens que si cette hypothèse est fausse.
Ce théorème décrit deux types de problème mathématique :
- Les problèmes dits « NP » qui sont l’ensemble des problèmes mathématiques dont la validation de la solution est rapide. C’est par exemple le cas pour la vérification de la validité du hash d’un block. Il suffit d’appliquer la fonction de hash aux données du block est de s’assurer que les deux hash sont identiques.
- Les problèmes dits « P » qui représentent l’ensemble des problèmes dont la résolution est rapide. Par exemple notre tri des nombres en ordre croissant.

La facilité, ou rapidité caractérisant la classe « P » est définie par les problèmes solubles en temps polynomial, c’est-à-dire que les algorithmes les plus performants pour résoudre ces problèmes sont de complexité polynomiale.
La difficulté caractérisant la classe « NP » est définie par les problèmes résoluble en temps exponentiel ou supérieur. Leur capacité à être résolue devient très vite inaccessible en fonction de la taille des données de ces problèmes.
Se poser la question P = NP revient à se demander si tous les problèmes qui sont facilement vérifiables sont aussi facilement résolubles ? Auquel cas nous aurions de sérieux problèmes.
Enfin, il existe une troisième sous classes nommé « NP-complet ». Cette dernière regroupe tout les problèmes mathématiques pour lesquelles trouver un algorithme permettant leurs résolutions en temps polynomiales, reviendrait à prouver que P = NP et que cette résolution est dérivable à tout les autres problème « NP ». La «NP-complétude» du logarithme discret dans le cadre des courbes elliptiques est un sujet à débat chez les mathématiciens. Certains pensent l’avoir démontré, alors que les récentes découvertes et avancés en algorithmiques quantiques tendent à prouver que ce dernier ne l’est pas, relançant les recherches pour des fonctions à sens unique dont la résolution est «NP-complète».
Quelles conséquences pour la cryptographie et Bitcoin ?
À l’origine calculer le hash d’un block est un problème facilement résoluble et facilement vérifiable. C’est pour cette raison que l’application d’un “nonce” afin de trouver un hash validant un seuil cible à été implanté par Satoshi Nakamoto. Ceci permet d’apporter une complexité à la recherche d’un hash valide par les mineurs, c’est le fondement même de la preuve de travail.
Il en est de même pour la réversibilité de nos clés publiques, aujourd’hui le problème du calcul du logarithme discret est un problème de complexité exponentielle, mais il se pourrait qu’un jour un algorithme avec une complexité plus faible soit trouvé, rendant le temps de résolution faisable à l’échelle temporelle humaine.
Si l’on venait à prouver que P = NP, il serait donc théoriquement possible de trouver un algorithme pouvant casser la preuve de travail. Problème mathématique qui aujourd’hui n’est possible à résoudre que par la force brute.
Heureusement pour nous, la grande majorité des informaticiens, au sens de ceux qui étudient l’information, pense que P ≠ NP. Mais c’est un problème encore ouvert qui n’a toujours pas pu être démontré mathématiquement ! Et à l’instar de l’identité de Satoshi Nakamoto, il se pourrait même que cette égalité ne soit ni démontrable, ni indémontrable. Nous laissant pour toujours dans l’inconnu.
Incomplétude de Gödel
Non seulement les mathématiques ne savent pas prouver que les verrous calculatoires de la cryptographie sont immuables. Mais en prime, il se pourrait qu’elles soient dans l’incapacité totale de le savoir un jour.
Les mathématiques réposent sur des postulat élémentaires que nous nommons des axiomes. On peut les considérer comme les plus petites briques de Lego permettant la construction de tous nos théorèmes. En 1931, Kurt Gödel parvient à démontrer que cette construction à l’aide d’axiomes comporte deux failles. Dans tout système axiomatique, il est soit possible de découvrir des problèmes qui sont indécidables, donc ni démontrables, ni réfutables. Soit de réussir à démontrer et à réfuter une théorie en même temps, rendant notre système axiomatique incohérent.
Il existe donc une probabilité non négligeable que P = NP soit indécidable. Nous laissant pour toujours dans l’incompréhension et dans l’incapacité de prouver l’immuabilité des mathématiques de notre cryptographie actuelle.
Satoshi Nakamoto avait-il anticipé la mort de Bitcoin ?
Nous arrivons au postulat de base qui m’a permis d’agrémenter ma petite fiction afin de vous faire découvrir les méandres mathématiques les plus profonds derrière notre cryptomonnaie favorite. Le wallet de Satoshi ne serait-il pas une sorte de « bounty program » ayant pour objectif de pousser à la résolution du problème du logarithme discret via celle du problème P = NP ?
Aujourd’hui, 1 million de dollars en récompense attends quiconque sera en mesure de le prouver ou le réfuter. Mais c’est une somme bien faible quand sa validité serait potentiellement destructeur pour notre société. Le démontrer reviendrait à prouver que tous nos processus de chiffrements sont en fait faillibles. Impactant irréversiblement l’avenir de l’humanité.
Voici ce qui serait selon moi le plus gros budget sécurité de l’histoire. Le wallet de Satoshi, quelques 23 milliards de dollars protégeant non seulement Bitcoin, mais toute notre société moderne. C’est ici que nous rebouclons sur l’évènement perturbateur sonnant le début de cette fiction dont, je l’espère, vous en avez apprécié la narration.
Il se pourrait que Satoshi Nakamoto se soit fait la promesse de ne jamais toucher à une seule miette de son trésor (ce que l’on peut raisonnablement croire). En revanche, si demain nous constations un mouvement sur son portefeuille, il pourrait s’agir de l’action d’un mathématicien malveillant ayant trouvé un algorithme efficace pour inverser nos clés publiques via la résolution d’un des sept puzzle du millénaire.
Bitcoin, une technologie au créateur probablement inconnu à jamais, à la démontrabilité possiblement indécidable, et protecteur de notre société moderne. De quoi élever Satoshi Nakamoto au rang de divinité du metaverse.
31 Février 2023, 21h00’00” UTC-5, Block n°6 930 000 — Le dernier block précédent l’ultime halving vient d’être validé, et la dernière récompense en bitcoin, minée. Les 21 000 000 de bitcoin sont désormais extraits. Cette accélération du temps de minage des block a eu pour effet d’augmenter de manière vertigineuse la difficulté de minage, désormais il faudrait plus de mille an pour miner un block avec la puissance de calcul actuelle des mineurs. Le mineur anonyme en a profité pour se renommer “Satoshi, it’s over” avant de miner le dernier block et d’éteindre sa machine. Gardant secret l’algorithme utilisé pour casser SHA-256, les blocks ne sont à présent plus minables. Ce n’est pas seulement bitcoin en tant que monnaie qui vient de mourir, mais Bitcoin en tant que réseau.
Nakamoto s’effondre sur le sol avant de pouvoir terminer sa phrase. Toute la salle se lève et même les lumières stroboscopiques des flashs des journalistes n’osent briser le silence ayant envahit brusquement la pièce. Un médecin s’approche pour contrôler son pouls, le monde retient son souffle, mais c’est bien celui de Satoshi qui semble s’être arrêté. Malgré les tentatives de réanimations, rien ne semble pouvoir inverser la situation.
« 21h00, Mr Nakamoto vient de rendre l’âme » indique le médecin de la maison blanche d’une voix grave.
C’est ainsi que s’acheva l’existence de Satoshi Nakamoto, pseudonyme disparu au moment exact où son réseau décentralisé est devenu figé à jamais. Il ne restait plus que l’homme, le vrai, à visage découvert, gisant sur le sol, dont personne ne cherchera à découvrir l’identité, par respect pour ses idéaux et ce qu’il avait tenté d’accomplir.
République ou royaume ? Fromage ou dessert ? Actions ET cryptos ! Pourquoi choisir puisque vous pouvez avoir les deux sur la même plateforme ? Inscrivez-vous dès maintenant sur Trade Republic. Vous recevrez un cadeau de 20€ (sous condition de dépôt de 2000€) pour passer à l’action (lien commercial).
