Histoire des Automated Market Makers – Les AMM décodés

Dans la première partie, nous avons exploré les notions de liquidité d’un marché et de market making. Nous allons ici introduire le concept d’AMM (automated market maker ou faiseur de marché automatisé). Bien qu’on pourrait penser que les AMM sont apparus avec les cryptomonnaies, leur histoire est plus ancienne.

Introduction aux AMM (Automated Market Makers)

Le market making est un pilier crucial de la finance : il n’y a pas de liquidité sans market makers. Avec le développement des sciences informatiques durant le 20ème siècle, les market makers humains « traditionnels » ont été peu à peu remplacés par leurs homologues numériques. On parle ainsi d’AMM – automated market makers, ou faiseurs de marchés automatisés.

Ces algorithmes de market making ont les objectifs suivants :

• Apporter de la liquidité à un marché en finançant à la fois les deux côtés de la paire échangée (buy side et sell side, offre et demande) ;
• Atténuer les fluctuations du prix de l’actif ;
• Limiter le spread au fur et à mesure que les volumes d’échange augmentent sur le marché.

Nous allons étudier l’histoire des AMM, depuis leur enfance au début des années 2000 jusqu’aux derniers modèles de la finance décentralisée.

Les marchés prédictifs

Les AMM (automated market makers) ont tout d’abord été étudiés de façon extensive dans la théorie des jeux. Plus précisément, ils furent utilisés en premier lieu au sein des algorithmes pour les marchés prédictifs.

Un marché prédictif permet à ses participants de parier sur l’issue d’un événement à venir. Ces paris sont donc matérialisés par des échanges financiers, des trades.

Pour obtenir une estimation commune des probabilités des résultats d’un événement, interroger des individus à plusieurs reprises n’est pas suffisant. En effet, la participation peut être irrationnelle. C’est par exemple le cas des sondages.

Avec une incitation économique, les participants tendent à se comporter de manière rationnelle. C’est parce que les participants ayant une meilleure information que les autres (sur l’occurrence d’un événement) ont un intérêt économique à fournir une estimation honnête.

Les marchés prédictifs sont basés sur l’agrégation de l’information – les convictions des participants au marché quant au futur d’un événement – et sur les paris. Les traders échangent des contrats, et le prix de ces contrats indique la probabilité de l’issue de l’événement. Comprise entre 0 et 100%, cette probabilité représente l’estimation générale. C’est donc une forme de crowdsourcing. Elle est moins biaisée qu’un sondage, grâce à l’incitation économique à agir de façon rationnelle et honnête.

Les options binaires représentent la forme la plus simple d’un marché prédictif. Elles sont aussi appelées « all-or-nothing options » (tout ou rien). Il s’agit d’un contrat qui, à expiration, règle un prix de 0 ou de 100%. Le paiement est donc une somme fixe, ou rien du tout, en fonction de l’issue de l’événement sous-jacent.

Règle de notation (scoring rule)

Afin de calculer le prix d’un contrat sur un marché prédictif, nous avons besoin d’une règle de notation ou scoring rule. Les règles de notation furent utilisées dès la fin du 20ème siècle pour obtenir des estimations de probabilité, par exemple dans la météorologie, les prévisions économiques ou encore l’analyse de risques. Cependant, ces modèles, et même les plus complexes, n’étaient pas satisfaisant en termes de convergence vers un prix d’équilibre.

Les chercheurs s’aperçurent que les marchés spéculatifs (tels que les actions, les commodités ou les contrats à terme) étaient beaucoup plus efficaces pour transformer des agrégats d’informations en prix.

C’est spécialement le cas des paris, même en cas de comportement irrationnel de certains participants. C’est ainsi que naquit l’idée de combiner règles de notation (scoring rules) et paris (betting markets). Après avoir combiné les deux de façon empirique, il apparut que c’était le meilleur moyen d’obtenir des estimations fiables.

Le premier modèle d’AMM : le modèle LMSR

Le premier modèle d’AMM est basé sur les LMSR. Le sigle signifie Logarithmic Market Scoring Rules for Modular Combinatorial Information Aggregation. On peut le traduire par « règles de notation logarithmique d’un marché pour l’agrégation d’information combinatoire et modulaire ». Le chercheur et professeur d’économie Robin Hanson le proposa en janvier 2002.

Règles de notation du marché

Une règle de notation d’un marché (market scoring rule) combine le meilleur des estimations de probabilité individuelles et des estimations de groupes, à travers les paris. Le modèle logarithmique préserve la probabilité de l’issue d’un événement donné, indépendamment des paris dépendant d’autres événements. Ce modèle est conçu pour les marchés prédictifs. Il optimise l’agrégation d’information et l’élicitation de probabilité.

De nombreux marchés prédictifs crypto utilisent aujourd’hui des versions améliorées de ce modèle. Il existe d’autres modèles pour des marchés où l’agrégation d’information est cruciale, et où les profits dérivent de l’habilité à évaluer les probabilités de la survenue d’événements futurs.

« En pratique, les règles de notation donnent de bonnes estimations de probabilité de la part des individus, tandis que les paris engendrent de bonnes estimations consensuelles des groupes. »

Robin Hanson

Dans le market making traditionnel, quelques acteurs centralisés (les market makers) fournissent de la liquidité de chaque côté du marché. Ils ajustent leur prix en fonction de l’activité. C’est un moyen correct d’agréger l’information, cependant, ces règles de notation basiques sont unidimensionnelles. Les règles logarithmiques permettent d’obtenir le même degré de précision pour des dimensions supérieures.

Les AMM basés sur les LMSR permettent de disposer d’un nombre arbitraire d’agents algorithmiques et d’interactions, sans augmenter les coûts opératifs.

La règle logarithmique

La LMSR détermine une fonction de récompense pour chaque participant au marché. Elle les incite à agir de façon rationnelle.

• Soit X une variable aléatoire indépendante, avec un espace de résultat fini Ω ;
• Soit p l’estimation de probabilité rapportée pour la variable aléatoire X.

Nous avons donc :

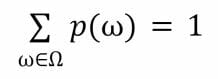
La fonction de récompense est définie ainsi :

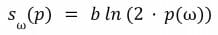
Où b > 0 est une constante. lorsqu’un participant au marché change l’estimation de probabilité courante p₁ vers p₂, il est récompensé s_ω (p₂) – s_ω (p₁) si l’issue de l’événement est ω. L’espérance de gain pour le participant est donc :

Ce modèle incite les participants à rapporter leur estimation de probabilité honnêtement afin de maximiser leur profit. D(p₂ || p₁) est appelé l’entropie relative ou la distance de Kullback Leibler entre les probabilités p₁ et p₂.

Un marché basé sur une LMSR peut donc être considéré comme :

• Une séquence de règles de notation logarithmiques où le market maker paie le dernier participant, et reçoit un paiement du premier participant ;
• Un market maker offrant |Ω| valeurs mobilières (securities). Chaque security correspond à l’issue d’un événement, et paye 1 $ si elle se réalise.

Changer la probabilité de ω ∈ Ω en une valeur p(ω) équivaut à acheter la security pour ω jusqu’à ce que le prix de marché de la security atteigne p(ω).

Le modèle LMSR et la finance décentralisée (DeFi)

Il est possible d’appliquer le modèle LMSR dans la finance décentralisée, pour obtenir une fonction de prix (cost function) pour chaque jeton listé sur un exchange. Cependant, comme nous allons le voir, ce n’est pas idéal, et ce n’est pas résistant au money pumping.

Soit un market maker proposant n catégories de jetons. Soit q = (q₁, …, q_n) où q_i représente le nombre de jetons correspondant à la catégorie i.

La fonction de coût est la suivante :

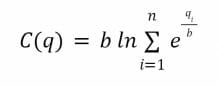
Pour chaque jeton, la fonction de prix est alors la suivante :

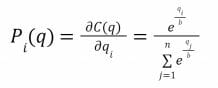
Il s’agit donc de l’inverse généralisé de la règle de notation.

• La fonction de coût fixe le montant total des actifs misés sur le marché, où C(q) est la subvention maximale du market maker ;
• La fonction de prix P_i(q) donne le coût courant d’un achat d’une quantité infinitésimale de jetons de la catégorie i.

Lorsqu’un trader désire modifier la quantité de parts d’actifs de q₁ vers q₂, il doit payer la différence des coûts C(q₁) – C(q₂).

Augur et Gnosis, deux plateformes de marchés prédictifs basées sur Ethereum, utilisent le modèle LMSR. Il est bien conçu pour ce cas d’usage particulier. Cependant, le modèle LMSR ne convient pas à la plus répandue des applications DeFi : l’échange de jetons à travers un AMM.

Voici les graphes des fonctions de prix pour 2 jetons et pour 3 jetons (i=2 et i=3). Dans le cas de 2 jetons, la fonction est une courbe; pour 3 jetons, il s’agit d’une hypersurface de dimension 3.

Le premier graphe représente la fonction de prix C (x, y, z) = 100 pour 3 jetons. Le second la fonction de prix C(x, y) = 100 pour deux jetons.

Le money pumping

Nous pouvons voir que le prix de chaque jeton fluctue légèrement seulement sur une petite partie de la courbe (coin supérieur droit), dans le cas où les réserves de chaque jeton sont équitablement distribuées. En dehors de cette partie, la droite de tangente devient verticale ou horizontale. Cela signifie qu’un trader peut utiliser une petite quantité d’un des jetons pour acheter tous les jetons restants dans le pool de liquidité.

C’est ce que l’on appelle le money pumping : nous en avons ici un exemple dans la finance décentralisée.

Ainsi, pour les applications d’échange de jetons (token swap) dans la DeFi, le modèle LMSR n’est pas utilisable. Les market makers courraient à leur perte, et le seul paramètre b contrôle trop d’aspects du comportement du market maker. Cela nous amène à une autre version du modèle : le liquidity-sensitive LMSR.

Liquidity-sensitive AMM – LS-LMSR

La sensibilité à la liquidité ou liquid sensitivity signifie qu’un échange (trade) de taille donnée influence moins le prix d’un actif sur un marché liquide que sur un marché illiquide.

C’est la propriété désirée pour la fonction de prix d’un AMM. En 2010, Abraham Othman and Tuomas Sandholm proposèrent un modèle liquidity-sensitive pour les AMM. Il est capable d’ajuster la réponse du prix au niveau d’intérêt actif du marché (l’activité de trading). C’était une grosse amélioration, car les prix ne fluctuent pas trop lorsque de gros trades sont effectués sur le marché. A contrario, les AMM simplistes étaient des agents de market making algorithmiques qui fournissaient toujours une réponse identique sans se soucier de l’activité du marché.

Cependant, il est difficile de transformer une règle de notation de marché en règle sensible à la liquidité. Sans trop entrer dans les détails mathématiques, voici comment cela se passe avec le modèle LMSR.

Le LS-LMSR change la constante b des formules du LMSR en la somme suivante :

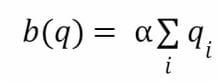
Où α est une constante.

La fonction de coût doit toujours progresser dans l’espace des obligations. Ainsi, spécifiquement, pour q = (q₁, …, q_n) la fonction de coût est :

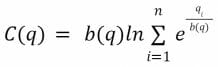
Cette variante du LMSR ajuste de façon efficace le paramètre b en fonction de la quantité d’échanges ayant lieu sur le marché.

La fonction de coût doit toujours avancer dans l’espace. Spécifiquement, pour q = (q₁, …, q_n) la fonction de prix est la suivante :

Cette variante des LMSR ajuste donc de façon efficace le paramètre b comme fonction de la quantité de trades prenant place sur le marché.

Graphes des fonctions de prix LS-LMSR

Il y a cependant un autre obstacle à surmonter pour nos AMM : ce modèle de market maker sensible à la liquidité peut s’avérer très lent. C’est le cas lorsqu’il faut s’adapter à des sauts importants de la valeur de l’actif sous-jacent. Ainsi, ce modèle déraille lorsque la valeur de l’actif varie brutalement après qu’une importante quantité de trading a eu lieu.

Market makers bayésiens

Les faiseurs de marché bayésiens (Bayesian Market Makers ou BMM) sont dédiés aux marchés prédictifs dont l’issue est binaire (0 ou 1). Un BMM fournit de la liquidité en adaptant son spread en fonction du niveau d’incertitude quant à la vraie valeur des actifs sous-jacents.

Dans de tels modèles, les fournisseurs de liquidité déposent tout d’abord leurs actifs en utilisant un ratio fixe. Ils fixent donc la distribution initiale des convictions quant aux résultats possibles. Ensuite, l’algorithme de l’AMM fournit la règle de notation. Il spécifie le coût nécessaire pour modifier la distribution des convictions de l’état courant vers le nouvel état souhaité. Cette scoring rule va inciter les traders à donner leur sentiment réel, afin que l’espérance de gain de l’ajustement de la distribution soit positive.

L’état de l’exchange (de la plateforme) dépend seulement de la quantité totale d’actifs déposés.

De plus, fixer le prix d’un échange requiert une unique fonction d’évaluation. Ce n’est pas le cas des algorithmes de correspondance des ordres (matching) plus complexes des carnets d’ordres.

Usage des BMM

Ces algorithmes bayésiens sont conçus pour prédire l’issue d’un ensemble d’événements disjoints, non pas pour définir un prix spécifique pour un actif. Ils ne peuvent donc pas être directement utilisés pour fixer les prix d’une paire de trading. De même, ils ne permettent pas d’attirer la liquidité avec des mécanismes suffisamment incitatifs pour les market makers.

Les premiers AMM pour la DeFi ont donc utilisé de nouveaux modèles. Avec ces systèmes, la fonction de prix (pricing function) spécifie le cours d’un actif en se basant sur la quantité totale disponible, et non pas en spécifiant le coût du changement d’une distribution donnée – l’état de l’AMM.

La fonction en question est appelée bonding curve (courbe de liaison). Le prix d’équilibre résultant est égal au prix du marché sous certaines conditions. Cependant, avec les modèles basés sur une bonding curve, nous avons besoin de pouvoir changer la quantité d’un actif pour pouvoir mesurer son prix.

Bancor : le premier AMM sur Ethereum

Le protocole Bancor représente la première tentative de bâtir un AMM pour les échanges de jetons ERC-20 sur Ethereum. Ce mécanisme d’accès aux liquidités est basé sur le concept de smart tokens – jetons intelligents.

Ces jetons verrouillent et conservent des réserves d’un ou plusieurs jetons ERC-20. Les utilisateurs les achètent ou les vendent afin d’accéder aux réserves de liquidité. Les prix sont déterminés par une formule spéciale.

Eyal Hertzog, Guy Benartzi et Galia Benartzi proposèrent le concept le 30 mai 2017. Leur whitepaper s’intitule Continuous Liquidity and Asynchronous Price Discovery for Tokens. Ce modèle simple de market making pour l’échange d’ERC-20 introduisit le premier mécanisme de découverte de prix pour l’échange de jetons sur Ethereum.

Le ratio de réserve constant

La méthode de découverte des prix est basée sur un ratio de réserve constant – Constant Reserve Ratio ou CRR. Ce ratio est défini par le créateur d’un smart token. La formule de Bancor l’utilise en combinant la quantité de smart tokens et le solde des réserves.

Prix = Solde / (Quantité * CRR)

Avec cette formule, le ratio entre les jetons en réserve et la capitalisation totale du smart token (quantité * prix) reste donc constant. Le prix du jeton en réserve est ainsi obtenu en divisant la market cap par la quantité (supply).

• Lors de l’achat de smart tokens (avec la réserve d’ERC-20), la quantité correspondante d’ERC-20 est ajoutée à la réserve. Cela accroît donc son solde. Les nouveaux smart tokens sont donnés à l’acheteur selon le prix déterminé par la formule.
• Lors de la vente de smart tokens, ces derniers sont brûlés. Le solde en ERC-20 correspondant au prix déterminé par la formule est transféré au liquidateur.

Lorsque le CRR tombe au-dessous de 100 %, l’achat de smart tokens entraîne l’augmentation du prix du jeton en réserve. Inversement, la liquidation de smart tokens entraîne la baisse du prix de l’ERC-20 correspondant.

Théoriquement, la formule permet de ne jamais vider la réserve de jetons, tout en gardant le CRR constant. Cependant, il y a toujours une différence entre un modèle théorique et son implémentation pratique.

Ainsi, le prix courant des smart tokens est censé être constamment ajusté en fonction des volumes d’achat et de liquidation. Il s’agit d’un modèle de découverte des prix asynchrone : en effet, le prix est calculé après chaque exécution d’ordre.

Ce faisant, le prix effectif est calculé comme fonction de la taille de la transaction.

Prix par transaction

Soient :

• R : le solde du jeton en réserve ;
• S : la quantité de smart tokens ;
• F : le ratio de réserve constant (CRR).

La quantité de smart tokens reçue en échange d’une quantité E de jetons ERC-20 en réserve est donc :

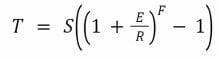
De même, la quantité de jetons ERC-20 obtenue en échange d’une quantité T de smart tokens est :

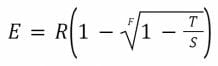
Bancor fut le premier AMM déployé sur Ethereum. Ce protocole peut ainsi être considéré comme le point de départ de la finance décentralisée. Cependant, il présente des limitations.

Les limites du protocole Bancor

La première version du protocole Bancor présentait de nombreux désavantages. Certains sont faciles à déceler :

• Exposition à de multiples jetons : les fournisseurs de liquidité doivent apporter chaque jeton ERC-20 présent dans les pools ;
• Slippage : puisque le ratio entre les réserves d’ERC-20 et la quantité de smart tokens est fixé, les gros trades vont impacter significativement la différence entre le prix courant du jeton et le prix effectif du trade ;
• Pertes impermanentes (impermanent loss) : nous parlerons de ce concept plus en détails. Résumons-le ainsi : lorsque le prix d’un jeton déposé en réserve dévie de son prix lors du dépôt, le fournisseur de liquidité recevra un solde plus faible lorsqu’il voudra récupérer ses jetons.

Il y avait également d’autres défauts de conception qui furent très vite exploités. Ce protocole définit un ancrage dynamique pour les jetons échangés via les réserves de jetons BNT (les smart tokens). Si les réserves sont faibles, les prix offerts par l’AMM pour les nouveaux jetons seront également très bas. Il est toujours possible d’acheter ou de vendre auprès du contrat, même s’il n’y aucun trader avec qui échanger. Les prix déterminés par l’AMM sont indépendants du marché global du jeton en question. Ainsi, l’AMM suit le marché, et ne le fait pas tendre vers l’équilibre. Plus grande est la différence entre le prix offert par Bancor et le prix au marché, plus il sera coûteux pour les réserves de l’AMM de s’aligner avec la vraie valeur de l’actif. En cas de panic sell (vente panique) sur le marché, l’AMM va épuiser ses réserves.

Avec les versions 2 et 3 de Bancor, ces inconvénients furent mitigés par divers mécanismes. Toutes ces expériences (et leur lot d’erreurs) ont permis à l’écosystème de la finance décentralisée d’améliorer ses protocoles.

En conclusion

Vous connaissez désormais l’histoire des AMM dans le monde merveilleux des cryptomonnaies et de la DeFi. Dans la troisième partie de cette série, nous allons explorer en détails les spécifications d’un modèle d’AMM bien connu, qui a révolutionné la finance décentralisée : l’AMM à fonction constante, incarné par Uniswap.

Bibliographie

• http://mason.gmu.edu/~rhanson/mktscore.pdf
• http://www.eecs.harvard.edu/cs286r/courses/fall12/papers/bmm-ec.pdf
• https://cryptorating.eu/whitepapers/Bancor/bancor_protocol_whitepaper_en.pdf
• https://www.cs.cmu.edu/~sandholm/liquidity-sensitive%20AMMs%20via%20homogeneous%20risk%20measures.wine11.pdf
• https://www.cs.cmu.edu/~sandholm/liquidity-sensitive%20automated%20market%20maker.teac.pdf