Zero knowledge proofs : Comprendre les preuves à divulgation nulle de connaissance : ZK-SNARKs, ZK-STARKs

Très connues dans le domaine des cryptomonnaies anonymes, les preuves à divulgation nulle de connaissance sont des outils cryptographiques très puissants. Elles permettent de prouver que l’on connaît une information, ou qu’une information est correcte, sans avoir pour autant à révéler cette dernière.

De la confidentialité à la scalabilité, leur champ d’application est vaste. Les types de preuves les plus connues sont les zk-SNARKs, utilisées sur ZCash, PivX, ou encore Mina Protocol (voir ici notre tuto pour déployer un node MINA). Plus récemment, les ZK-STARKs ont fait leur apparition sur Ethereum, grâce à l’entreprise Starkware. Pour comprendre leur fonctionnement, il faut étudier quelques exemples et faire un peu de mathématiques.

Les zero-knowledge proofs (ZKP), ou comment prouver la véracité d’une proposition sans la connaître

Une preuve à divulgation nulle de connaissance est un protocole cryptographique qui permet de prouver la véracité d’une proposition sans avoir connaissance de la proposition elle-même.

Un “fournisseur de preuve” peut prouver mathématiquement à un “vérificateur” l’exactitude d’une information, sans révéler quoi que ce soit d’autre que sa véracité et son intégrité.

Les preuves à divulgation nulle de connaissance doivent satisfaire trois propriétés :

• La consistance (completeness) : si le fournisseur de preuve et le vérificateur suivent le protocole, alors le vérificateur doit toujours accepter la preuve ;
• La robustesse (soundness) : si la proposition est fausse, aucun fournisseur de preuve malveillant ne peut convaincre un vérificateur « honnête » que la proposition est vraie, et ceci avec une forte probabilité ;
• La divulgation nulle d’information (zero knowledge) : le vérificateur n’apprend, de la part du fournisseur de preuve, rien de plus que la véracité de la proposition.

Il existe plusieurs méthodes pour construire des preuves à divulgation nulle de connaissance. Initialement, les protocoles nécessitaient une interaction entre le prouveur et le vérificateur (preuves interactives). Aujourd’hui, ils existent sous forme non-interactive.

Afin de comprendre le système, Jean-Jacques Quisquater et Louis Guillou ont proposé un exemple dans leur article de 1989 intitulé « How to explain zero-knowledge protocols to your children ». On parle de protocole Sigma ou engagement-défi-réponse.

L’exemple de Guillou-Quisquater

Soient Alice, le fournisseur de preuve, et Bob, le vérificateur. Considérons une grotte, présentant une bifurcation (chemin A et chemin B). Pour passer de A à B ou de B à A, il faut ouvrir une porte grâce à un mot magique.

Alice veut prouver à Bob qu’elle connaît le mot magique pour ouvrir la porte, mais sans que Bob ne l’apprenne.

Il s’agit d’une preuve de connaissance, car Alice prouve à Bob qu’elle connaît le mot magique, mais sans divulgation d’information, puisqu’Alice ne révèle pas ce mot secret.

Engagement, défi et réponse

Alice et Bob vont alors répéter plusieurs fois le scénario suivant :

• Engagement : Bob reste à l’extérieur de la grotte, et ne voit pas l’intérieur du tunnel. Alice entre dans la galerie et choisit aléatoirement le chemin A ou B (par exemple en tirant à pile ou face).

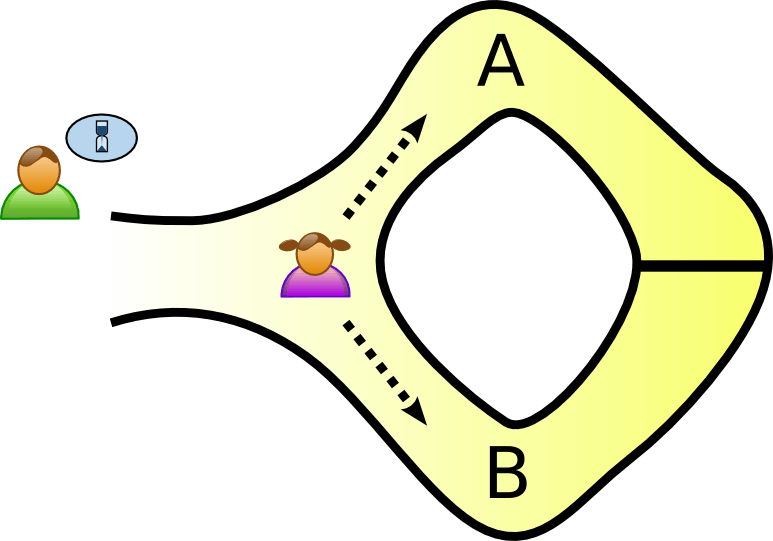
• Défi : Bob entre dans la grotte, et se place au niveau de la bifurcation. Après avoir tiré au sort un des deux chemins (A ou B), il crie le résultat à Alice.

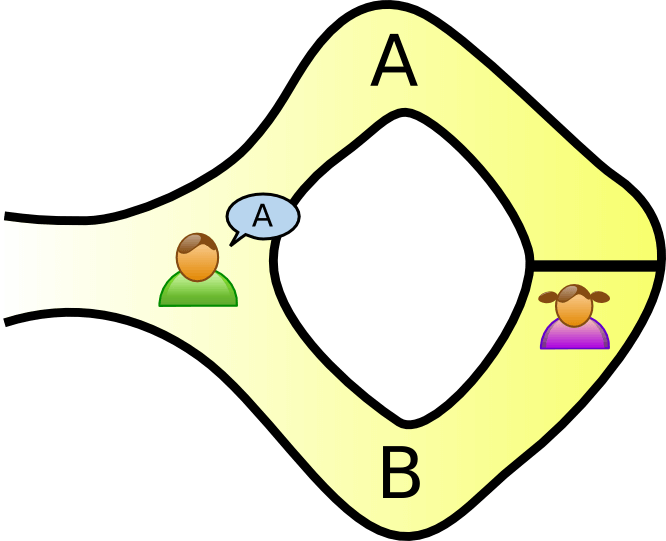
• Réponse : Alice doit prouver qu’elle est en possession du mot magique en sortant par le chemin demandé par Bob.

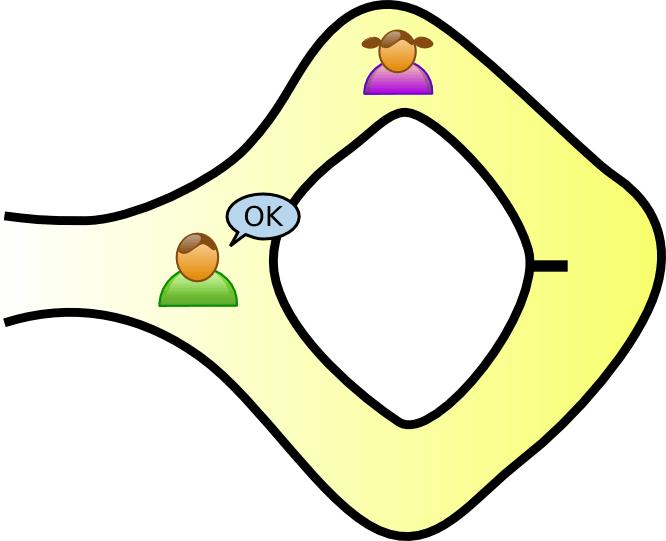
Il y a alors plusieurs possibilités.

Si Alice connaît le mot magique :

• Alice se trouve en A, Bob annonce B, et elle satisfait sa demande ;
• Elle se trouve en B, Bob annonce A, et elle satisfait sa demande ;
• Elle se trouve en A, Bob annonce A, et elle satisfait sa demande ;
• Alice se trouve en B, Bob annonce B, et elle satisfait sa demande.

Si Alice ne connaît pas le mot magique :

• Alice se trouve en A, Bob annonce B, et elle ne satisfait pas sa demande ;
• Elle se trouve en B, Bob annonce A, et elle ne satisfait pas sa demande ;
• Elle se trouve en A, Bob annonce A, et elle satisfait sa demande ;
• Alice se trouve en B, Bob annonce B, et elle satisfait sa demande.

Un protocole interactif

En partant du principe qu’Alice suit le protocole (consistance), Bob sera certain qu’Alice ne connaît pas le mot magique si elle commet une erreur. Cependant, Bob peut être dupé dans le cas où Alice ne connaît pas le mot magique, mais où la demande de Bob correspond à sa position actuelle.

Bob va alors répéter le schéma à partir de la première étape. À chaque itération, il va renforcer la fiabilité de la preuve. Si Alice n’est pas en possession du mot magique, il y a 50 % de chance pour qu’elle commette une erreur. Avec N itérations, la probabilité que Bob affirme qu’Alice possède le secret alors qu’elle ne le possède pas est de ( 1 / 2^N ).

Comme nous allons le voir, les protocoles interactifs ont un inconvénient. Penchons-nous sur un schéma d’authentification classique, les signatures de Schnorr.

Le protocole d’authentification de Schnorr

Le protocole de Schnorr est l’une des premières applications des preuves à divulgation nulle de connaissance. Ce schéma de signature numérique pourrait notamment être implémenté sur Bitcoin pour le rendre plus confidentiel. Faisons un peu de mathématiques pour voir comment il fonctionne en version interactive.

Ce protocole repose sur le problème du logarithme discret : il s’agit de prouver que l’on connait un élément x appartenant à un groupe G, engendré par g, étant donné g^x .

Soient un nombre premier q et un groupe G engendré par g, d’ordre q. On dit que g est générateur d’un sous-groupe, d’ordre q, de G. g et q sont publics.

Alice souhaite alors prouver à Bob qu’elle connaît un élément x tel que y = g^x

• Engagement : Alice tire de façon aléatoire un nombre entier s dans l’ensemble Z*_q et le garde secret. Elle va ensuite calculer v = g^s et l’envoyer à Bob.

• Défi : Bob tire ensuite aléatoirement à son tour un entier c dans Z*_q et l’envoie à Alice.

• Réponse : Alice calcule r = s – cx et l’envoie à Bob.

Par substitution, puisque r = s – cx et y= g^x alors : g^(s-cx)* g^cx = g^s = v

Bob vérifie donc que v = g^r * y^c. Si c’est le cas, alors Alice connaît bien x.

Les inconvénients des protocoles interactifs

Ces protocoles sont dits interactifs, car le fournisseur de preuve et le vérificateur doivent communiquer entre eux pour se livrer à ce jeu d’engagement-défi-réponse. Cela présente un inconvénient majeur : le fournisseur de preuve et le vérificateur doivent être en ligne au même moment.

C’est ainsi que les chercheurs Fiat et Shamir ont proposé un protocole non-interactif en 1986. Il a servi de fondation aux preuves utilisées sur Mina, les zk-SNARKs. Pour arriver à leurs fins, les chercheurs israéliens ont utilisé les fameuses fonctions de hachage.

La transformation de Fiat-Shamir : rendre les preuves non-interactives

L’heuristique de Fiat-Shamir est une méthode qui consiste à simuler la présence du vérifieur de preuve : il est ainsi remplacé par une fonction de hachage cryptographique. Pour rappel, une fonction de hachage est à sens unique. Il est impossible, à partir de l’image de la fonction (le hash), de calculer les données d’entrées.

• Lors de la phase d’engagement, le fournisseur de preuve va générer un élément a.
• Lors de la phase de défi, il hache c = H (a, x) et va calculer une réponse r correcte pour le défi c. Il envoie ensuite π = (a, r) comme preuve.
• Lors de la phase de réponse, le vérificateur exécute la fonction de hachage sur (a, x) pour calculer c et vérifier que r est bien une réponse correcte pour le couple (a, c).

Schéma de signature

La fonction de hachage permet de s’assurer que le fournisseur de preuve n’a pas pu tricher. S’il l’on reprend le protocole d’authentification de Schnorr, voici comment se déroule le schéma de signature non-interactif :

• Alice souhaite toujours prouver qu’elle connait x tel que y = g^x dans un groupe G engendré par g, d’ordre q. g et q sont publics.
• Génération des clefs : Elle va tirer au hasard un entier s et calculer t = g^s . s est secret, il s’agit de sa clef privée. En revanche, Alice publie t, sa clef publique.
• Défi et réponse : Alice calcule ensuite c = H (g,y,t) où H est une fonction de hachage publique. Enfin, elle calcule r = v – c*x. Le couple (c,r) représente sa signature.

Bob, comme tout ceux qui ont accès aux variables publiques (g, q t, H, c et r), peuvent vérifier que t = g^r * y^c, donc qu’Alice connaît bien s, et authentifier sa signature (c, r).

La transformation de Fiat-Shamir permet donc de se passer d’interaction entre fournisseur de preuve et vérificateur. Ces preuves satisfont bien les trois propriétés fondamentales recherchées :

• Consistance : Bob peut être convaincu de l’honnêteté d’Alice si la relation t = g^r * y^c est vraie.
• Robustesse : il est impossible pour Alice de générer une preuve correcte sans posséder sa clef privée.
• Divulgation nulle de connaissance : il est impossible pour Bob de calculer la clef privée d’Alice à partir des données publiques.

Dans le cas des zk-SNARKs (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge), les preuves sont non-interactives et succinctes.

Les zk-SNARKs : des preuves à divulgation nulle de connaissance légères et non-interactives

Dans le cas des zk-SNARKs, les preuves sont succinctes (la taille des preuves générées est très réduite – quelques kilooctets) et non-interactives (le protocole ne nécessite pas d’interaction entre le fournisseur de preuve et le vérificateur). Alice et Bob sont remplacés par des algorithmes qui génèrent et vérifient les preuves dans des délais rapides, pour les adapter aux cas d’usage et aux propriétés des blockchains (confidentialité, scalabilité).

Un protocole à non-divulgation de connaissance basé sur les zk-SNARKs repose sur trois algorithmes :

• Le générateur de clefs : l’algorithme génère deux clefs, la clé de preuve et la clef de vérification. Ces clefs sont générées en injectant un paramètre secret λ au sein du programme. λ doit absolument rester confidentiel, sinon, il serait possible de fabriquer de fausses preuves.
• Le fournisseur de preuve : l’algorithme va générer la preuve à partir de 3 entrées. Tout d’abord, la clef de preuve; ensuite, l’entrée x publique, et enfin, la déclaration privée, dont il veut prouver la connaissance, sans révéler de quoi il s’agit réellement.
• Le vérificateur : l’algorithme de vérification fournit en sortie une variable booléenne (« vrai » ou « faux »). En entrée, il faut y injecter la clef de vérification, la preuve générée par le fournisseur, et l’entrée publique x.

L’aspect non-interactif de ce schéma permet alors de générer et diffuser des preuves cryptographiques sur un réseau distribué, et de permettre aux nœuds de ce réseau de vérifier ces preuves de façon indépendante et sans avoir à interagir avec l’entité qui les a généré.

L’intérêt des zk-SNARKs et leurs applications dans l’univers des cryptomonnaies et des blockchains commence alors à sauter aux yeux.

Les preuves SNARK appliquées aux cryptos

Les ZKP permettent de vérifier la validité d’une séquence de calculs, impliquant des données confidentielles, sans avoir à révéler ces dernières ou à refaire les calculs.

Par exemple, on peut prouver la validité d’une transaction sans avoir à révéler son montant, les parties impliquées ou autre information sensible.

Dans le domaine des cryptomonnaies, c’est l’équipe de ZCash qui utilisa en premier les propriétés étonnantes des zk-SNARKs afin de créer des transactions confidentielles, les shielded transactions. Grâce aux preuves, les nœuds validateurs du réseau peuvent vérifier qu’une transaction est valide sans connaître son montant ou les adresses impliquées.

Génération des clefs et trusted setup

Les paramètres secrets utilisés pour la génération des clefs doivent être inconnus de tous, pour qu’il ne soit pas possible de forger de fausses preuves.

Le fournisseur de preuve et le vérificateur doivent donc s’accorder un ensemble de connaissances communes sur la façon dont les preuves sont générées. Généralement, ces informations sont encodées via une chaîne de référence commune ou CRS (Common Reference String). Cela sert à prouver que les clefs de preuve et de vérification sont générées par le même algorithme.

Afin de garder les preuves « succinctes« , c’est-à-dire pour que leur taille varie de façon sous-linéaire en fonction de la quantité de calcul menée, il faut encoder la relation dans une chaîne structurée de référence – Structured Reference String ou SRS – qui fait partie de la CRS. En quelque sorte, les preuves subissent un prétraitement.

Les différentes implémentations

ZCash est la première cryptomonnaie qui a implémenté les zk-SNARKs. Basée sur la confidentialité des transactions, les preuves permettent d’échanger de la valeur de pair à pair, et de façon anonyme. Les nœuds validateurs du réseau peuvent vérifier que les signatures des transactions sont correctes, sans autre divulgation. Le système de preuves SNARKs de ZCash est basé sur un trusted setup, célèbre au sein de la communauté crypto.

Si les paramètres secrets tombent entre de mauvaises mains, il est possible de forger des fausses preuves. L’équipe de ZCash les a donc généré de façon collaborative (multi-party computation) lors d’une célèbre cérémonie. Avec ce type de protocole, tous les participants doivent être compromis ou malhonnêtes pour modifier à leur avantage les paramètres finaux. Les nombres aléatoires ayant servi à générer les paramètres, ainsi que les ordinateurs utilisés, ont été détruits.

Créé plus récemment, Mina Protocol utilise les zk-SNARKs pour maintenir sa blockchain, une blockchain « succincte », la plus légère en existence. Au-delà d’une taille très réduite (22 ko) offrant un grande scalabilité au réseau, Mina innove : leurs ZK-SNARKs sont relativement légères et ne nécessitent pas de trusted setup.

Les applications décentralisées sur Mina sont nommées les Snapps. Elles permet d’imaginer de nouveaux types de services et d’applications, préservant la confidentialité des données utilisateurs. Les possibilités dans le domaine de l’authentification numérique sont multiples.

Les zk-SNARKs sont sophistiquées. Cependant, elles sont loin de représenter la solution parfaite. Tout protocole de preuve à divulgation nulle de connaissance est un compromis entre la confidentialité du fournisseur de preuve, et l’assurance qu’il ne peut pas tricher, pour le vérificateur. En outre, la phase de trusted setup n’est pas idéale en termes de transparence.

Les ZK-STARKs : des preuves transparentes

Si les paramètres générés durant le trusted setup sont compromis, les preuves n’ont plus de valeur. Les ZK-SNARKs nécessitent donc de faire confiance à une tierce partie. Les cryptologues souhaitaient trouver un moyen de générer des ZKP sans passer par un intermédiaire de confiance. C’est dans ce but qu’une équipe de chercheurs israéliens, Eli Ben-Sasson (fondateur de Starkware), Iddo Bentov, Yinon Horesh et Michael Riabzev, ont conceptualisé un nouveau type de ZKP.

Dans leur papier du 6 mars 2018, les chercheurs présentent les ZK-STARKs. L’acronyme signifie « Zero-Knowledge Scalable Transparent ARguments of Knowledge« . Elles sont supérieures aux ZK-SNARKs en plusieurs points :

• Tout d’abord, les ZK-STARKs ne nécessitent pas de trusted setup (transparent). Elles s’appuient sur les fonctions de hachage dans le modèle de l’oracle aléatoire ;
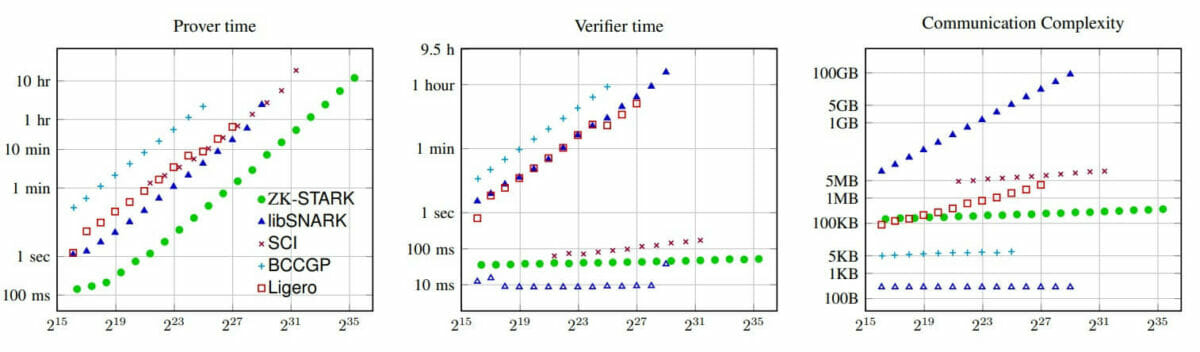
• Ensuite, les STARKs sont beaucoup plus rapides à vérifier, et leur taille est plus faible (scalable) ;
• Enfin, elles sont résistantes aux calculateurs quantiques (quantum-resistant), contrairement aux SNARKs.

Le modèle de l’oracle aléatoire

Un oracle aléatoire est un modèle théorique, idéalisé, qui est utilisé en cryptologie pour prouver la sécurité d’un algorithme. On peut le visualiser comme un oracle que l’on interroge et qui fournit toujours une réponse aléatoire.

Il s’agit du comportement idéal d’une fonction de hachage :

• Elle est déterministe : un même antécédent (entrée, préimage) donne toujours la même valeur de hachage (image, sortie) ;
• Cette valeur de hachage peut être calculée facilement ;
• Il est impossible, connaissant cette image, de retrouver l’antécédent (résistance à la préimage) ;
• Pour une entrée donnée, il est impossible d’en trouver une autre ayant la même valeur de hachage (résistance à la seconde préimage) ;
• Deux entrées différentes ne peuvent jamais donner la même valeur de hachage (résistance aux collisions) ;
• Une légère modification de l’entrée modifie considérablement la valeur de hachage.

Certaines fonctions de hachage ne suivent pas le cadre de l’oracle aléatoire. Elles ne sont donc pas considérées sûres.

Les IOP (Interactive Oracle Proofs)

Les preuves STARK sont interactives, et utilisent un oracle aléatoire lors de leur phase de vérification. Cela confère un énorme avantage : leur scalabilité. En effet, la vérification des preuves est très rapide, et la durée de cette vérification croît sous-linéairement linéairement en fonction de leur taille.

Applications des ZK-STARKs dans les cryptos

Du fait de leur excellente scalabilité, les ZK-STARKs sont avant tout utilisées pour créer des solutions de couche secondaire pour les blockchains. C’est notamment le cas de Starkware où les ZK-STARKs sont à la base de ses produits StarkNet et StarkEx, des layers 2 pour Ethereum.

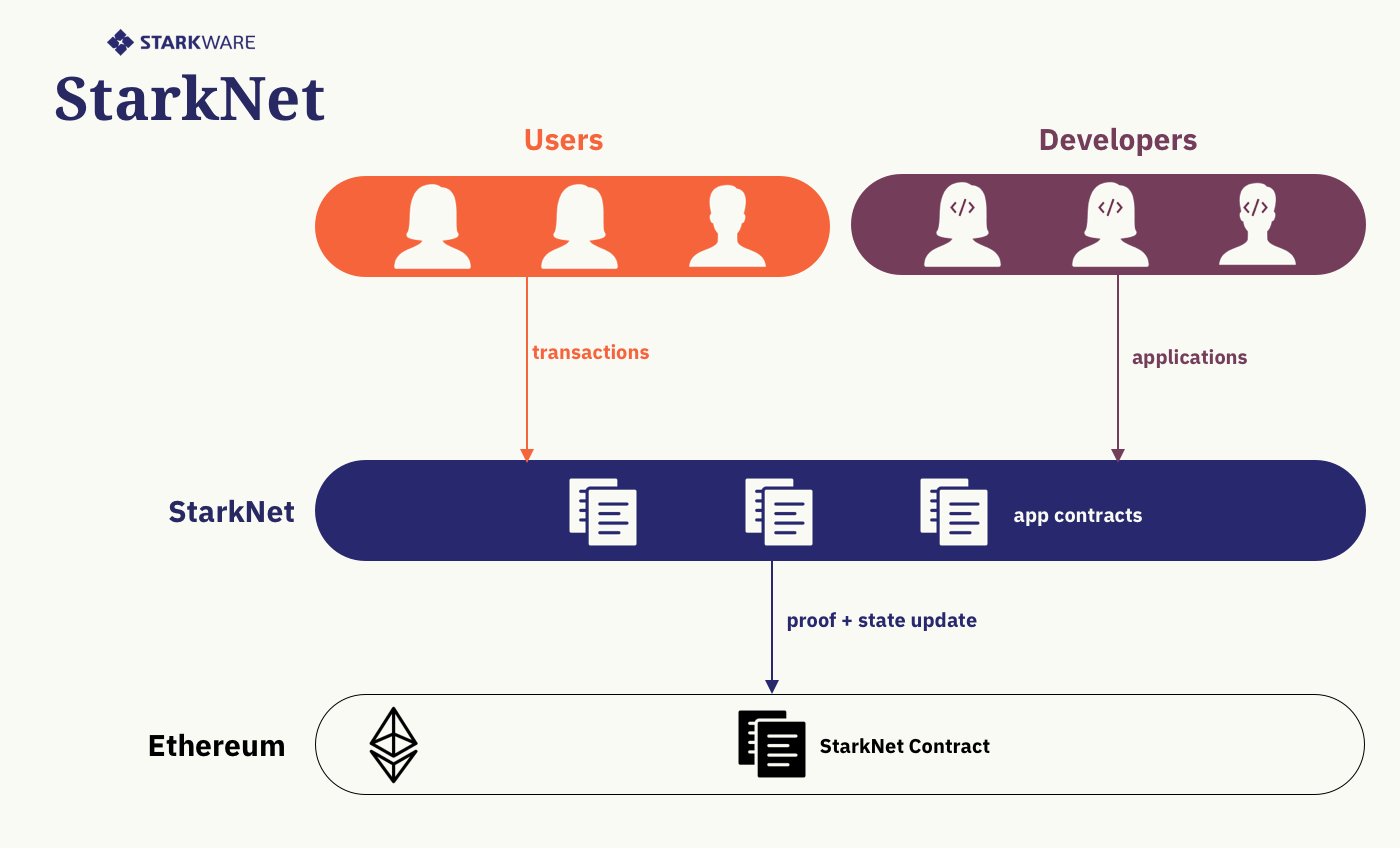
StarkNet est une plateforme basée sur les ZK-Rollups. Elle permet de prendre en charge les mêmes calculs et opérations que le réseau-mère, avec le même degré de sécurité, mais avec beaucoup plus de scalabilité.

Les opérations qui se déroulent sur StarkNet sont agrégées. Ces agrégats sont alors assortis d’une preuve cryptographique de leur validité. Les nœuds d’Ethereum peuvent ensuite la vérifier, puis mettre l’état de la blockchain à jour.

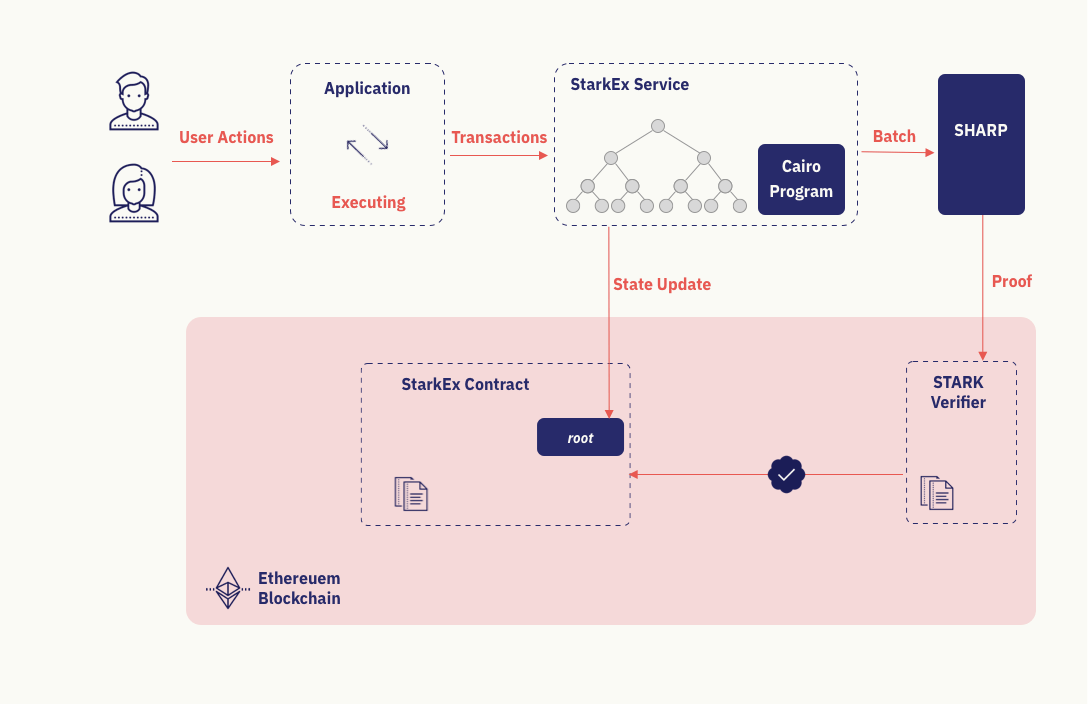
Quant à StarkEx, il s’agit d’un moteur destiné à rendre Ethereum scalable, grâce aux STARKs. Les nœuds de la seconde couche génèrent les preuves off-chain, qui seront ensuite vérifiées on-chain.

En conclusion

Les preuves à divulgation nulle de connaissance sont bien trop complexes pour faire l’objet d’un simple article, et il faut considérer celui-ci très superficiel. Ce champ de la cryptologie obsède les plus brillants chercheurs de la planète depuis des années. Grâce aux cryptomonnaies, les théories élaborées sont mises en pratique. En effet, derrière les ZKP se cache le graal de l’anonymat et de la protection de la vie privée des utilisateurs d’un réseau décentralisé. De même, la scalabilité des blockchains sera grandement améliorée grâce aux solutions de couche secondaire qui utilisent ces outils mathématiques. Leurs applications sont autant de nouveaux continents à explorer pour les années à venir !

Ressources

• How to Explain Zero-Knowledge Protocols to Your Children – Jean-Jacques Quisquater, Louis Guillou
• Scalable, transparent, and post-quantum secure computational integrity – Eli Ben-Sasson, Iddo Bentov, Yinon Horesh, Michael Riabzev
• What are zkSNARKs? The Comprehensive Spooky Moon Math Guide – Ameer Rosic