Ferveo : une égide infranchissable contre les mineurs opportunistes

Anoma est une nouvelle cryptomonnaie promettant des évolutions majeures, qui la considèreraient comme la première véritable cryptomonnaie de troisième génération. Après le Bitcoin représentant la première génération et l’Ethereum représentant la deuxième, ce serait Anoma qui serait au centre de la troisième génération. Tout cela a été expliqué avec deux vidéos que nous avons publiées précédemment (première ici et deuxième là), mais ces dernières ne sont pas suffisantes pour vraiment tout savoir à propos d’Anoma. Aujourd’hui, nous allons vous présenter plus en détail une des innovations qu’Anoma apportera au monde de la crypto : Ferveo, leur système de protection contre la Valeur Extractible par les Mineurs (ou Maximale, si vous préférez).

En effet, la VEM est un problème majeur pour les utilisateurs, notamment parce que les cryptomonnaies sont quasiment toujours des réseaux financiers avant tout. On ne compte plus le nombre de victimes de sandwich trading bots sur les plateformes d’échange décentralisées, par exemple… Bien sûr, on a quelques mécanismes de protection intégrés sur certaines applications (cf. protection contre le slippage sur Uniswap), mais de manière générale, il faudrait trouver un moyen de combattre la VEM à la source, plutôt que de s’occuper des symptômes. Et, c’est là que Ferveo entre en jeu.

Partage de clé secrète de Shamir

L’idée derrière Ferveo est très simple : la VEM existe uniquement parce que tous ceux qui le désirent ont la possibilité de voir le contenu des transactions avant qu’elles soient publiées. Par conséquent, pour supprimer totalement la VEM, il suffit de rendre le contenu des transactions totalement incompréhensible avant la publication.

Pour y parvenir, les créateurs d’Anoma ont recouru au partage de clé secrète de Shamir. C’est un procédé mathématique très bien conçu et permettant à un groupe de personnes de se partager une information secrète, pour qu’il soit impossible pour un petit nombre d’entre eux de déchiffrer le secret.

Pour être plus exact, voilà comment ça fonctionne. Imaginons qu’il y a 100 personnes qui souhaitent se partager un secret α, qui est un élément d’un corps fini F, pour que n’importe quel sous-ensemble de 67 personnes déchiffre le secret, en empêchant tout sous-ensemble de 66 personnes et moins d’obtenir une quelconque information relative au secret.

En principe, le détenteur initial du secret α, auquel tout le monde fait confiance, génère un polynôme p(x) tel que p(x) = α + α₁ x + α₂ x² + … + α₆₆ x⁶⁶.

Au sein dudit polynôme, α₁ et suivants sont des éléments choisis aléatoirement dans le corps fini F.

Lorsque ce calcul a été fait, le détenteur initial du secret qui a créé le polynôme peut distribuer à chaque personne un résultat de p(i), avec i = 1 pour la première personne, 2 pour la deuxième personne, etc. Ces résultats sont appelés des évaluations.

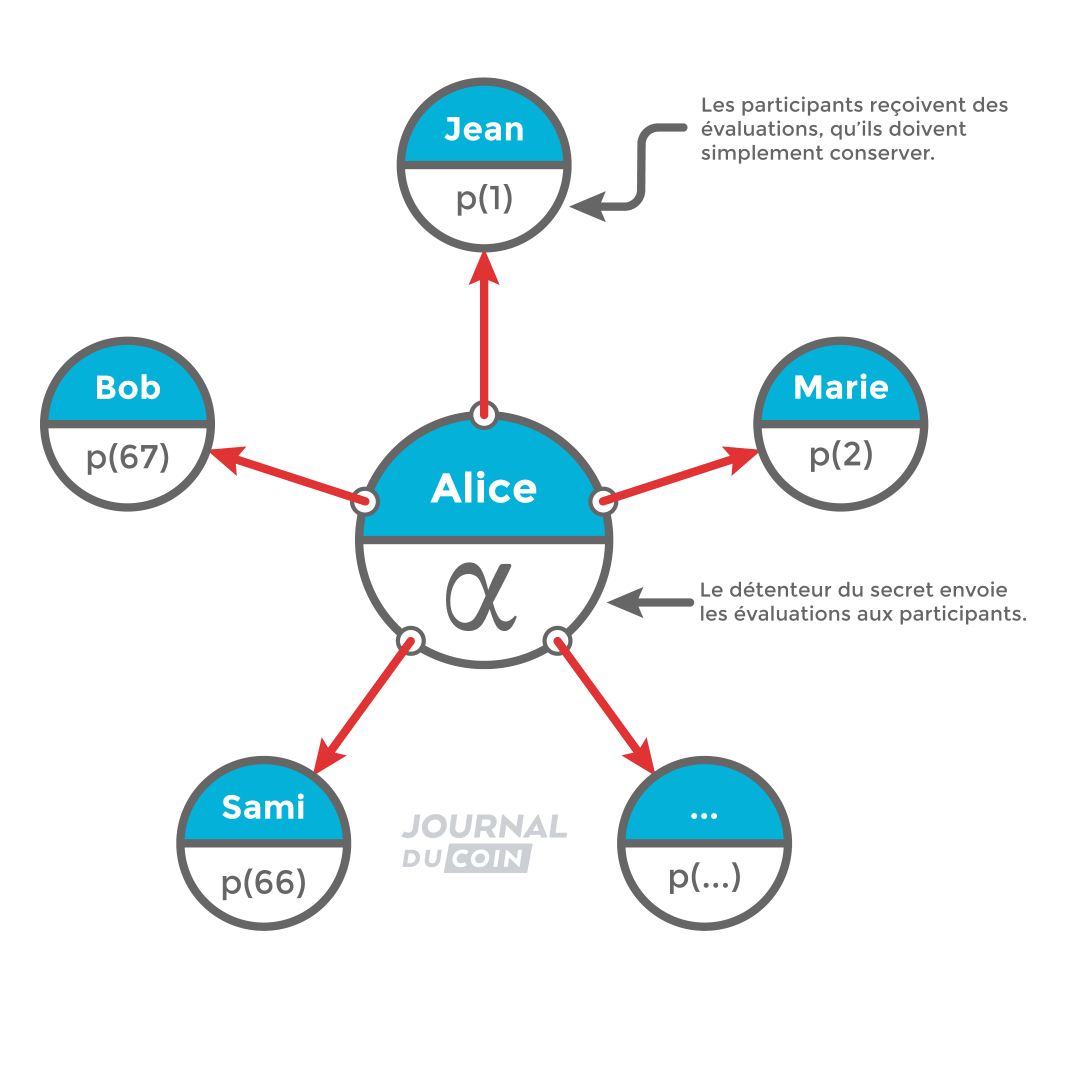
Dans ce contexte, p(0) représente en fait le secret déchiffré : α₁ à α₆₆ sont multipliés par zéro, il ne reste que le secret α. L’avantage, c’est que comme il y a un nombre incroyable de valeurs possibles pour α₁ à α₆₆, connaître p(i) ne nous apprend rien tant que i n’est pas égal à zéro. En effet, peu importe le nombre de personnes qui assemblent leurs fragments de secret, tant qu’ils sont moins de 67. Il y aura toujours |F| polynômes potentiels correspondant aux fragments dont ils disposent, chacun de ces polynômes potentiels ayant une valeur différente lorsque i = 0. Par conséquent, tout ensemble de 66 personnes ou moins ne détient en vérité aucune information utile vis-à-vis du secret α.

C’est seulement lorsque 67 personnes réunissent leurs évaluations qu’elles peuvent déterminer la valeur du secret.

Grâce au partage de clé secrète de Shamir, nous avons donc un moyen de découper un secret en morceaux, de sorte qu’il soit impossible pour une minorité de déchiffrer l’information. Mais, il y a un gros problème : ce mécanisme requiert la présence d’une autorité centralisée ! En l’occurrence, il s’agit du créateur du secret qui doit également fragmenter la clé et la distribuer aux participants. Sur les réseaux crypto, il ne peut exister aucune entité du genre. Et, si d’aventure, c’était le cas, navré de vous en informer de cette manière, mais vous êtes client d’une banque, pas utilisateur d’un réseau crypto.

Heureusement, le partage de clé secrète de Shamir n’est pas rendu obsolète par cet obstacle : il suffit d’avoir également recours à un mécanisme de génération de clé distribuée, ou distributed key generation (DKG) en anglais.

Génération de clé distribuée

Ce second élément consiste en vérité à demander à tous les participants de générer leur propre polynôme. En effet, avec le partage de clé secrète de Shamir, s’il n’y a qu’un seul participant qui se charge de la génération du polynôme, il pourrait envoyer des évaluations falsifiées provenant de différents polynômes, il pourrait envoyer des évaluations seulement à certains participants et ne rien faire parvenir à d’autres… En bref, tel qu’il est, ce système ne marche pas très bien sur un réseau décentralisé.

C’est pour cela que nous devons recourir à la génération de clé distribuée. Cette dernière nous permet de construire un système devant respecter trois caractéristiques très importantes :

• Elle permet à tous les détenteurs d’évaluations de vérifier que leur évaluation provient du même polynôme p,
• Elle permet à tous les détenteurs d’évaluations de vérifier que tout le monde a bien reçu son évaluation,
• Elle ne permet à personne de connaître la clé privée générée de cette manière sans réunir autant d’évaluations que nécessaire.

Si l’on parvient à créer un système atteignant ces trois objectifs, alors on pourra l’utiliser avec le partage de clé secrète de Shamir dans le contexte d’un réseau décentralisé.

Vérification de l’origine des évaluations

Pour que chaque participant puisse vérifier qu’il n’a pas reçu une évaluation sans aucun rapport avec le polynôme p, le système utilisé sur Ferveo recourt à une technique cryptographique plutôt récente. La mise en gage polynomiale, ou polynomial commitment en anglais. La théorie des mises en gage existe depuis 1988, et la version dite « KZG » qui est l’une des plus connues date seulement de 2010.

Pour faire simple, elle consiste à calculer une valeur y à partir d’un secret β et du polynôme choisi, puis à fournir cette valeur y à un tiers qui la gardera secrète. Plus tard, lorsque le secret β est révélé, le tiers pourra également révéler la valeur y pour prouver que le secret β n’a pas été modifié entretemps. . En effet si le système est bien fait, il est impossible de trouver un autre polynôme avec lequel on obtient la même valeur de mise en gage.

Grâce à ce type de mécanisme, tous les détenteurs d’évaluation peuvent vérifier que leurs évaluations ont la même origine.

S’assurer que tout le monde a bien reçu son évaluation

Pour éviter qu’un créateur de secret omette de transmettre une évaluation à l’un des participants, il faut pouvoir s’assurer que tout le monde en a reçu une. Cependant, on ne peut pas simplement publier les évaluations sans les chiffrer, puisque dans ce cas, tout le monde pourrait également déchiffrer le secret instantanément.

Inversement, on ne peut pas se contenter d’envoyer des versions chiffrées individuellement avec un algorithme de chiffrement classique. Le résultat ne serait pas vérifiable comme authentique par les autres participants. Malheureusement, de telles solutions nécessitent que certaines conditions soient réunies, et ce n’est pas idéal dans le contexte de la cryptomonnaie.

Heureusement, il existe déjà des mécanismes de partages de secrets publiquement vérifiables. On dit que ce sont des mécanismes de PVSS, pour public verifiable secret sharing. Et certains systèmes DKG rentrent dans cette catégorie, sous certaines conditions (utilisation d’un couplage avec une courbe elliptique compatible).

Avec ces systèmes « PVDKG », on peut chiffrer les évaluations de sorte à ce que seul le destinataire puisse les déchiffrer, en permettant tout de même à des tiers de vérifier que l’évaluation chiffrée est compatible avec la valeur mise en gage précédemment.

Maintenant, nous avons presque tout ce qu’il faut, mais il reste un problème : nous n’avons décrit, jusqu’ici, que des systèmes où il y a une entité unique qui détient le secret α et qui produit les évaluations p(i) à envoyer aux autres participants. Comment faire pour appliquer ça à un système décentralisé ?

Faire en sorte que personne ne connaisse la clé privée

En fait, la solution est plus simple qu’il n’y paraît. Pour que personne ne connaisse la clé privée, il suffit que tout le monde génère son propre secret et ses propres évaluations. C’est possible grâce au fait que le PVSS est un système de chiffrement homomorphe additif, c’est-à-dire que l’on peut additionner deux polynômes en additionnant les coefficients correspondants pour obtenir les coefficients du nouveau polynôme. Par ailleurs, une évaluation à la valeur i du nouveau polynôme est égale à la somme des évaluations à la valeur i des deux polynômes d’origine… Fait qui se vérifie également pour les mises en gage.

Il est donc possible d’ajouter des coefficients, des évaluations ou mises en gage pour en obtenir d’autres parfaitement valides. Concrètement, si 67 participants génèrent chacun leur propre polynôme et l’ajoutent à celui des autres, alors le résultat final est un polynôme qui demeurera secret tant que les 67 ne se mettront pas d’accord pour le déchiffrer.

Cela étant dit, vous vous êtes certainement déjà rendu compte du problème que ça entraîne : il faut que tous les participants communiquent entre eux, beaucoup plus qu’avec un seul secret, pour vérifier que tout est valide. Ce n’est donc pas adapté aux réseaux avec une très grande quantité de validateurs.

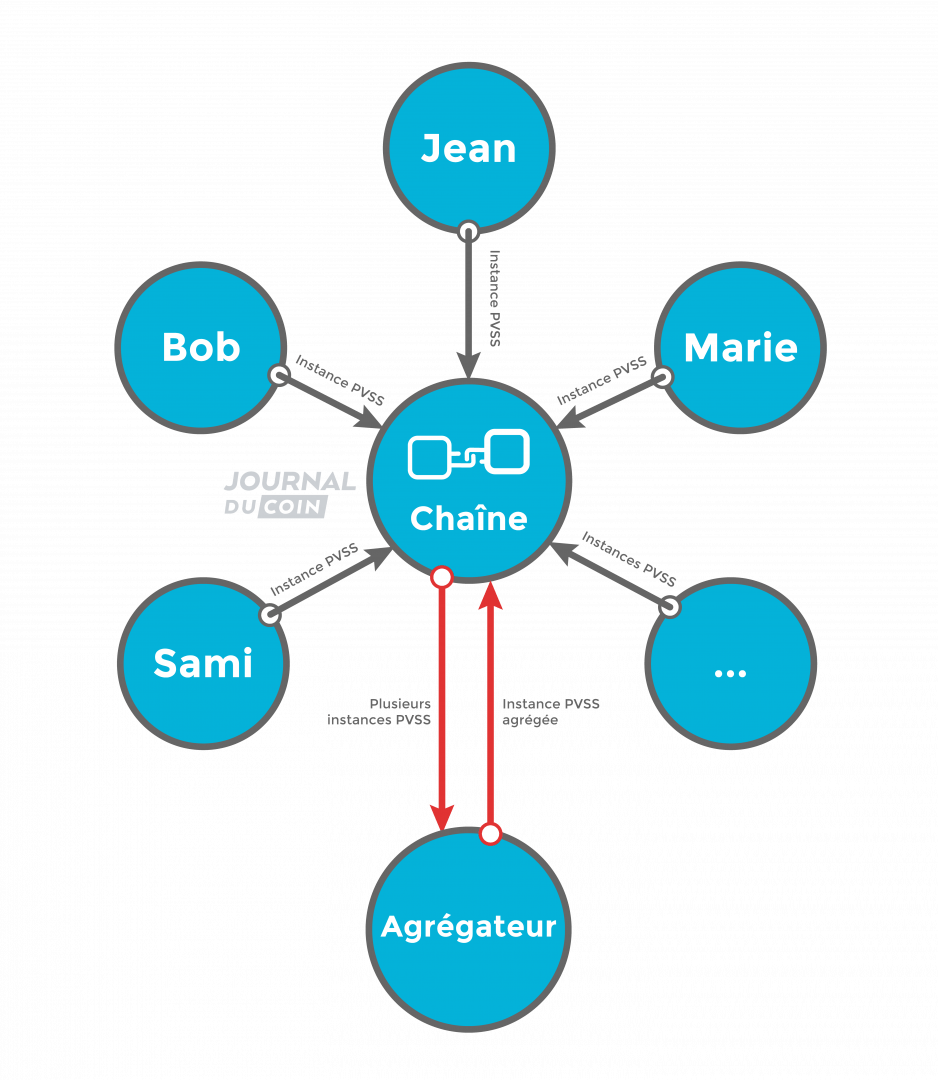
La solution à cet inconvénient réside dans le livre blanc « Aggregatable Distributed Key Generation ». En effet, en ayant recours à un agrégateur PVSS auquel tous les participants font parvenir les données en les publiant sur la blockchain, le processus de vérification ne doit être fait qu’une fois. Et, lorsque l’agrégateur a publié le résultat agrégé sur la blockchain, les participants n’ont qu’à vérifier s’ils le souhaitent que la version agrégée est valide et que tout a été fait dans les règles.

En résumé, voilà comment ça fonctionne : les participants doivent d’abord publier sur la blockchain un paquet de données comprenant une mise en gage polynomiale, ainsi que l’ensemble des évaluations de p(x), chiffrées pour que seuls leurs destinataires puissent les consulter individuellement. Et comme indiqué précédemment, il est possible pour tous les participants de vérifier que chaque évaluation provient du même polynôme grâce à la valeur mise en gage qui a été publiée. Nous appellerons donc ces paquets de données des instances PVSS.

Ensuite, l’agrégateur (un participant comme les autres quand il s’agit d’un réseau décentralisé) récupère des instances publiées sur la blockchain, et publie une instance PVSS agrégée. Ce procédé peut être réalisé en plusieurs étapes, avec un agrégateur différent à chaque étape. Par exemple, le premier agrégateur pourrait agréger 10 instances PVSS, et le suivant pourrait prendre cette première agrégation et y ajouter 5 instances PVSS supplémentaires… Jusqu’à ce que l’on arrive à une instance PVSS agrégée finale représentant les 67 instances PVSS émises par les participants. Avec cette méthode, l’une des parties les plus complexes du procédé PVSS est accomplie beaucoup plus vite.

La limite majeure de ce système, c’est qu’il ne fonctionne pas sur une chaîne asynchrone. Mais les chaînes basées sur Tendermint ne sont pas concernées, et Anoma (qui est basé sur Tendermint aussi) est donc parfaitement compatible avec.

Cryptographie de seuil et questions pratiques

Lorsque l’agrégation a été faite, on obtient une clé publique, et les validateurs obtiennent chacun une évaluation correspondant à une part de clé privée.

La clé publique, d’abord, sera nécessaire aux utilisateurs, qui s’en servent pour chiffrer leurs transactions et obtenir ainsi un message chiffré C.

Une fois que les messages chiffrés C₁, C₂ et suivants sont parvenus aux validateurs, ces derniers utilisent chacun de leur côté la part de clé privée dont ils disposent. En déchiffrant les messages chiffrés avec cette part de clé privée, ils génèrent des parts de transaction déchiffrée, qu’ils combinent ensuite à celles obtenues par les autres validateurs.

Avec ce procédé, on ne fait que déchiffrer les transactions une par une. On n’a donc pas besoin de révéler la clé privée pour déchiffrer les transactions. De cette manière, l’ensemble clé publique/clé privée généré grâce au processus PVDKG peut être réutilisé pendant quelques temps.

Dans le cas d’Anoma, cette durée sera approximativement de 24 heures. En effet, c’est aussi la durée d’une epoch sur le réseau. Toutes les 24 heures, de nouveaux validateurs peuvent arriver dans la liste de ceux autorisés à créer des blocs.

Maintenant, imaginons. Si, par exemple 50 validateurs sortaient de la liste, mais que l’on gardait la clé privée existante, alors il serait impossible de valider des transactions par la suite. En effet, il resterait moins de 67 validateurs actifs disposant d’une part de clé. 

Voilà pourquoi il est obligatoire de refaire la procédure de création de clé publique/privée toutes les 24 heures. Cela signifie que les utilisateurs devront aussi régulièrement vérifier la clé publique devant être utilisée pour chiffrer les messages. En principe, les portefeuilles comme Metamask s’en chargeront automatiquement, donc ce n’est pas vraiment un problème.

Cependant, il faut noter qu’il y a un autre inconvénient à ce système et qui est plus dérangeant pour les utilisateurs lambda. Ce problème trouve son origine dans le fait que lorsqu’un utilisateur utilise une clé publique trop vieille pour chiffrer sa transaction, le message chiffré en résultant sera invalide. Par conséquent, un utilisateur publiant une transaction chiffrée à la fin d’une epoch et ayant choisi de payer peu de frais de gas pourrait voir sa transaction rejetée par le réseau, si le changement de clé publique/privée a lieu avant la publication de sa transaction.

En d’autres mots, il ne sera pas possible d’économiser en publiant une transaction très peu rémunératrice pour les validateurs, si le réseau est vraiment surchargé pendant 24 heures. Contrairement à Ethereum qui peut parfois laisser vos transactions flotter dans la mempool pendant des jours avant de les valider, les réseaux utilisant Ferveo auront une limite de facto correspondant à la longueur d’une epoch.

Cela étant dit, en principe, ça ne deviendra pas un problème sur la vaste majorité des réseaux utilisant Ferveo, puisqu’il s’agira probablement de chaînes basées sur Anoma. Non seulement ces dernières seront conçues pour supporter une quantité de transactions assez grande sans que les coûts augmentent vraiment, mais en plus, Anoma dispose du système d’instances fractales permettant de mieux résister à ces problèmes : si le réseau est surchargé, il suffit de créer une nouvelle subdivision sous la forme d’une instance fractale.

Pour protéger les utilisateurs de la VEM dont ils souffrent sur quasiment tous les réseaux de cryptomonnaies, Ferveo est incontestablement l’un des meilleurs, si ce n’est le meilleur système imaginé jusqu’à maintenant.

Il a quelques inconvénients, mais ces derniers ne devraient pas avoir d’impact significatif sur l’expérience utilisateur en principe, contrairement aux avantages massifs apportés. Et si vous souhaitez en savoir encore plus au sujet de Ferveo, n’hésitez pas à aller lire le livre blanc dédié, qui vous dira à peu près tout ce que vous devez savoir.