Scroll et sa zkEVM : make Ethereum great again !
La course à la scalabilité d’Ethereum passe par des solutions dites « de couche secondaire » (layer 2). Ces infrastructures permettent d’alléger la charge de la blockchain principale (layer 1). Parmi les techniques utilisées, les ZKP (preuves à divulgation nulle de connaissances) sont réputées efficaces et sécurisées.
Nous vous présentons Scroll, une toute nouvelle solution de scalabilité basée sur ces fameuses preuves. Elle embarque une machine virtuelle intégrant ces fameuses preuves, offrant une compatibilité native pour tous les smart contracts Ethereum existants. Pour comprendre le fonctionnement de Scroll, de ses zkRollups et de sa zkEVM, suivez le guide.
Table des matières
- Scroll : son équipe et sa vision
- Principes techniques de Scroll
- Philosophie et conception de Scroll
- La scalabilité d’Ethereum avec Scroll : zkEVM et zkRollups
- Scroll et les challenges de la zkEVM
- Les piliers techniques de Scroll
- Fonctionnement de Scroll
- Conception de la zkEVM de Scroll
- L’architecture générale de Scroll
- Fonctionnement des zkRollups de Scroll
- Génération et coût des preuves sur Scroll
- Utiliser Scroll et participer à son développement
- Ressources et bibliographie
Scroll : son équipe et sa vision
Scroll est un projet cofondé par 3 entrepreneurs et scientifiques : Sandy Peng (université de Cambridge), Haichen Shen (universités de Tsinghua et de Washington) et Ye Zhang (universités de Pékin et de New-York).
L’équipe endosse les valeurs originelles d’Ethereum : une plateforme accessible, tant en termes d’expérience utilisateur que de frais. Elle a donc choisi de travailler à améliorer sa scalabilité à travers ces fameuses couches secondaires (L2).
Il existe différentes manières d’agréger des transactions sur une couche secondaire. Scroll repose sur les zkRollups. L’équipe de développement est convaincue qu’il s’agit de la solution la plus efficace à ce jour. Elle a donc conçu une machine virtuelle pour Ethereum basée sur ces preuves : une zkEVM.
Ethereum pour tous
Le but ultime des développeurs d’Ethereum est de rendre le réseau accessible à un très grand nombre de personnes. Pour cela, il faut grandement améliorer la scalabilité du système. Il s’agit à la fois de permettre au réseau principal (L1) d’exécuter toujours plus d’opérations, mais aussi d’offrir des frais minimes.
Afin libérer le potentiel d’Ethereum, les applications décentralisées (dApps) actuelles doivent pouvoir être utilisées avec des frais et une rapidité optimale. Les L2 répondent à cet objectif – particulièrement ceux qui sont basés sur les ZKP, tels StarkNet ou Kakarot. Mais encore faut-il que la conception de dApps sur ces L2 soit abordable pour les développeurs. C’est le but de la zkEVM de Scroll : permettre à tout développeur Ethereum de portabiliser son code sur le L2 – Scroll.
Un développement open-source
La team Scroll est particulièrement attachée aux idéaux du développement et open-source. Elle est ainsi attentive aux autres solutions de L2, et collabore avec d’autres membres de la communauté.
Le code de Scroll est public et auditable : c’est un gage de sécurité – n’importe qui peut le relire ou participer à son amélioration.
Décentralisation et résistance la censure
Ce sont deux piliers fondamentaux d’Ethereum. La recherche d’une meilleure scalabilité ne doit pas se faire aux dépens de la décentralisation et de la résilience du réseau. Étant donné que le L1 d’Ethereum gère à la fois le consensus et la disponibilité des données, le niveau de sécurité de Scroll est le même.
La résistance à la censure d’un zkRollup est plus difficile à atteindre. Elle fait l’objet de recherches actives, notamment en utilisant l’accélération matérielle pour permettre aux utilisateurs de déployer leurs algorithmes de preuve eux-mêmes.

Principes techniques de Scroll
Scroll est conçu autour de quatre principes techniques fondamentaux pour l’équipe de développement du projet : sécurité, équivalence EVM, efficacité et décentralisation.
Sécurité de l’utilisateur
Pour tout utilisateur d’une solution de seconde couche, la sécurité de ses fonds (et de ses données personnelles) est primordiale. Scroll utilise donc le consensus de la couche de base d’Ethereum pour assurer la finalisation des transactions. Ainsi, il n’y a pas à faire confiance à des nœuds du L2 pour assurer l’intégrité des fonds des utilisateurs.
EVM-équivalence
L’idée est d’offrir la même expérience de développement sur un L2 que sur Ethereum. Afin de permettre aux programmeurs de migrer sans effort leurs applications décentralisées du L1 au L2, Scroll s’engage à maintenir un environnement de développement équivalent à l’EVM.
Les approches de L2 EVM-compatibles basées sur la transpilation posent des challenges en termes de sécurité. Avec sa pleine équivalence EVM, Scroll évite aux développeurs de modifier et d’auditer leur code.
Transpilation : compiler le code d’un langage à un autre source à source.
Efficacité
L’efficacité d’un L2 peut être évaluée en termes de débit et de frais de transactions :
- Les frais doivent être considérablement réduits par rapport à ceux du L1 ;
- La préconfirmation des transactions sur le L2 doit être quasi-immédiate, et leur finalisation sur le L1 raisonnablement rapide.
Le challenge est donc d’obtenir de bonnes métriques pour ces deux variables, sans toutefois sacrifier la sécurité du système. Bien qu’il soit beaucoup plus facile d’obtenir un L2 efficace en opérant dans un environnement centralisé, ce n’est pas idéal en termes de sécurité. Scroll vise donc à proposer un environnement entièrement décentralisé, afin de bénéficier du plus haut degré de sécurité possible, celui du consensus d’Ethereum.
Décentralisation
L’équipe de Scroll considère la décentralisation d’un protocole comme une propriété essentielle. En effet, un système décentralisé sera robuste et résistant aux attaques (en particulier aux attaques coordonnées et à la censure).
C’est donc à tous les niveaux que les développeurs souhaitent décentraliser Scroll :
- Opérateurs des nœuds ;
- Prouveurs ;
- Communauté (utilisateurs et développeurs).
Cet objectif de décentralisation est l’une des raisons du développement open source de Scroll.

Philosophie et conception de Scroll
Les principes techniques sus-cités ont de nombreuses implications dans le design de Scroll.
Les zkRollups et la zkEVM
Les exigences en termes de sécurité et d’EVM-équivalence mènent ainsi à la conception d’un type adapté de zkRollup. Les preuves sont succinctes et sont vérifiées sur le L1 d’Ethereum. Toutes les transactions effectuées sur le L2 présentent donc le même degré de sécurité que celles du L1.
Quant à l’équivalence EVM, l’idéal était bien sûr de créer une zkEVM, ce qui relève de la prouesse technique. Fort heureusement, les récentes avancées des chercheurs dans le domaine des preuves à divulgation nulle de connaissance offrent cette possibilité.
Le réseau des prouveurs
C’est en ayant en tête l’objectif de décentralisation de Scroll, mais aussi pour obtenir un faible délai de finalisation des transactions que provient l’idée de créer un réseau de prouveurs dédié. Ce réseau décentralisé et sans permission sert à générer les preuves de validité des zkRollups.
Cette infrastructure est scalable : en effet, il suffit d’ajouter des nœuds prouveurs pour améliorer sa capacité de calcul des preuves. De même, les opérations effectuées par ces nœuds sont hautement parallélisables.
L’équipe de Scroll fournira tout d’abord des prouveurs GPU en open-source, mais elle compte sur sa communauté pour créer de meilleures solutions matérielles (basées sur les FPGA et les ASIC, par exemple).
Avec le temps et la compétition dans le domaine, la latence et le coût de la génération des preuves devraient grandement diminuer. L’équipe de Scroll compte également décentraliser le Séquenceur, pour améliorer encore la solidité et la résistance à la censure du protocole.
Recherche et innovation
Grâce à son développement open-source et transparent, la team Scroll a pu bénéficier des dernières innovations dans le domaine des ZKP, comme :
- L’amélioration des systèmes de preuves ;
- Les nouvelles méthodes d’agrégation des preuves ;
- L’accélération matérielle pour les ZKP.
Scroll travaille avec le PSE (Privacy and Scaling Explorations), le groupe de la Fondation Ethereum. Ce mode ouvert de recherche et développement devrait permettre de trouver les meilleures solutions dans le domaine. Actuellement, Scroll explore plusieurs axes d’amélioration :
- Les data blobs post-danksharding ;
- L’optimisation de la zkEVM, avec de nouveaux algorithmes ZK “hardware-friendly” ;
- La façon dont les primitives ZK sont présentées aux développeurs d’applications sur le Layer 2.
Scroll est donc parfaitement aligné avec les principes techniques mais aussi philosophiques de la communauté Ethereum. La scalabilité de “l’ordinateur universel” passera par les solutions de couche secondaire.
La scalabilité d’Ethereum avec Scroll : zkEVM et zkRollups
La machine virtuelle d’Ethereum ou EVM est l’environnement d’exécution du réseau, permettant d’y déployer des smart contracts. Son langage de programmation principal est Solidity. Une fois le code des contrats compilé (traduit en bytecode), l’EVM l’interprète, donc chaque opération a un coût en gas.
Les couches secondaires ou L2 permettent d’améliorer le débit d’Ethereum et de diminuer ses frais d’utilisation. Il existe plusieurs écoles : sidechains, chaînes Plasma ou rollups. Chacune offre ainsi un compromis en terme d’efficacité, scalabilité, de décentralisation et de sécurité.
Un rollup représente le nouvel état de la blockchain après un ensemble de transactions ayant eu lieu sur le L2 (un batch). Cet état est donc constitué des soldes des comptes utilisateurs et du code des smart conctracts concernés sur le L2. Plus précisément, le smart contract sur le L1 maintient une racine d’état : la racine de l’arbre de Merkle du rollup. Cela permet d’agréger des transactions sur le L2, et d’effectuer les transitions d’état sur le L1.

Scroll utilise un type particulier de rollup, basé sur les ZKP, d’où son nom : zkRollup. Les ZKP, pour zero-knowledge proofs, sont des preuves qui permettent d’attester de la validité de l’ensemble des transactions envoyées du L2 au L1.
Qu’est ce qu’un zkRollup ?
Les zkRollups sont considérés comme la solution de L2 la plus pertinente en termes de sécurité et de délai de finalisation. La preuve générée est succincte, c’est-à-dire que le L1 peut la vérifier rapidement et facilement. Cela permet d’agréger un grand nombre de transactions issues du L2. Il n’y a pas besoin de ré-exécuter ces dernières pour mettre à jour l’état de la blockchain : c’est ce qui rend les frais minimes.
Les zkRollups présentent toutefois des inconvénients :
- Ils doivent être codés dans un langage spécifique (R1CS) à la syntaxe lourde et demandant une expertise certaine ;
- Ils ne sont pas composables, c’est-à-dire qu’il n’est pas possible pour différentes applications décentralisées d’interagir entre elles sur un L2 de ce type.
L’objectif de Scroll est de fournir la meilleure expérience utilisateur pour développer avec les zkRollups sur Ethereum. L’idée est de rendre la vérification des preuves native au sein de l’EVM : les dApps du L1 pourront ainsi être portabilisées telles quelles, en utilisant des zkRollups. Il faut donc créer une EVM pouvant intégrer les opérations relatives aux ZKP.
Qu’est-ce qu’une zkEVM ?
Une zkEVM est une machine virtuelle pour Ethereum intégrant les calculs relatifs aux preuves à divulgation nulle de connaissance (ZKP).
Les zkRollups sont peu coûteux et sécurisés. Ils peuvent cependant présenter des problèmes de compatibilité. La team Scroll a donc créé une zkEVM pour rendre les dApps compatibles avec leur solution de couche secondaire.
Il y a deux manières d’utiliser Scroll : premièrement, l’ASIC (Application-Specific Circuit). Il s’agit de coder les contrats de façon spécifique à chaque application en utilisant le langage R1CS. On appelle ce code de bas niveau le circuit de base du rollup. Cependant, se posent les problèmes de la composabilité et de la pauvre expérience développeur.
À l’inverse, tout l’intérêt de la zkEVM est de pouvoir bénéficier de la même expérience de développement que sur la couche primaire d’Ethereum. Tous les langages EVM sont acceptés, à commencer par Solidity.
Une telle machine virtuelle tourne sur un CPU, il suffit donc de programmer un circuit CPU universel pour vérifier les opérations de bas niveau. Une fois ce circuit universel créé, on peut vérifier l’exécution de tout type de programme. Cependant, cette approche fut rejetée par le passé : le moindre opérande du circuit de base génère une multitude d’étapes au sein de l’EVM.
Un circuit arithmétique est le modèle standard pour effectuer, en calcul informatique, des opérations complexes sur des polynômes. En cryptographie et notamment dans le domaine des ZKP, les polynômes sont omniprésents. Nous y reviendrons plus tard !
Cependant, coder le smart contract dans un langage vérifiable par l’EVM est une approche coûteuse. Chaque opération nécessite des frais élevés côté prouveur, sur le L1.
Scroll base le compromis de sa solution sur une zkEVM, offrant une expérience de développement très simple, tout en optimisant les coûts d’exécution via son circuit EVM spécifique.
Scroll et les challenges de la zkEVM
Créer une zkEVM native relève pour l’instant de la prouesse. Techniquement, il faut résoudre de nombreux défis, tant au niveau de la conception que des mathématiques pures.
Les courbes elliptiques
L’EVM ne supporte pas les graphes de courbes elliptiques (cyclic elliptic curves), nécessaires aux ZKP. Cela rend difficile la création de preuves récursives ou de protocoles ZK spécialisés. Il faut donc que l’algorithme de vérification soit ajusté pour être EVM-compatible.
La taille des mots de l’EVM
Elle est actuellement de 256 bits. Les ZKP utilisent des opérations arithmétiques dans les champs premiers. Cette incompatibilité encombre considérablement la taille du circuit dans l’EVM, d’environ de ordres de magnitude. On parle de mismatched field arithmetic.
Les opcodes spéciaux de l’EVM
Les codes opératifs originaux de l’EVM demandent de nouveaux modèles de conception. Lors de la conception du circuit ZK, il faut tenir compte, par exemple, du gas et des fonctions call.
L’EVM est une machine à pile
L’EVM n’utilise pas un registre pour stocker ses données, mais une pile. Elle exécute toujours les premiers opérandes de la pile. Ce n’est pas le cas de la SyncVM de zkSync ou de l’architecture de StarkNet, qui fonctionnent avec un registre.
La couche de stockage d’Ethereum
La couche de stockage de l’EVM est basée sur Keccak et les MPT (Merkle Patricia Tries). Ces spécifications ne sont pas adaptées aux ZKP et font exploser les frais.
Il faut donc trouver des solutions à ces nombreux problèmes. Heureusement, la recherche dans le domaine des ZKP est prolifique, et des nouvelles techniques apparaissent, faisant grandement diminuer le coût de génération des preuves.

Les piliers techniques de Scroll
Scroll rassemble différents outils mathématiques pour optimiser la création des preuves.
La mise en gage polynomiale
Derrière ce nom barbare se cache une technique cryptographique nouvelle, qui permet une bonne flexibilité pour construire les ZKP. Il s’agit d’une amélioration par rapport au R1CS. En effet, le langage de bas niveau donne peu de place à l’optimisation car les contraintes doivent être de degré 2 (à cause des appariements de courbes elliptiques). Les schémas d’engagement polynômial permettent d’élever le degré des contraintes.
En mathématiques, une contrainte est une condition que doit satisfaire la solution d’un problème d’optimisation.
Une table de recherche efficace
L’utilisation d’une table de recherche (lookup table), conçue en Arya et optimisée en Plookup, permet de réaliser des économies substantielles. Ses arguments présentent une syntaxe agréable flexible, grâce à TurboPlonk et UltraPlonk. Cela permet de réduire fortement les surcoûts du circuit EVM.
Des preuves récursives abordables
Composer des preuves récursives était par le passé très coûteux. Une fois de plus, c’est dû aux opérations sur courbes elliptiques. Une nouvelles technique permet d’amortir les coûts : Halo. Quant à l’agrégation de preuves, Aztec permet d’améliorer la scalabilité du circuit.
La vérification des preuves par GPU
L’équipe de Scroll a conçu l’algorithme prouveur le plus rapide pour GPU et ASIC/FPGA. Pour donner un ordre de grandeur, il est au moins 5 fois plus rapide que celui de Filecoin. L’accélération matérielle rend la génération de preuves ZK beaucoup plus rapide.
Fonctionnement de Scroll
L’idée maîtresse est ainsi d’optimiser l’architecture du système pour réduire la taille du circuit arithmétique. Cette architecture spécifique réduit les coûts de production des preuves.
En pratique, la zkEVM de Scroll permet à tout développeur de compiler et de déployer son code, écrit dans un langage EVM, comme Solidity. Le bytecode correspondant est ensuite déployé sur le L2. L’expérience utilisateur sera la même que sur le L1, à une différence près : les frais sont considérablement réduits, tout comme le délai de pré-confirmation des transactions.
Flux au sein de la zkEVM
Au sein du L2, l’exécution d’un ensemble de transactions nécessite la preuve de validité du circuit zkRollup correspondant. En contrepartie, le L1 (Ethereum) réexécute les transactions pour s’assurer de leur validité et mettre à jour l’état de la chaîne.
Sur le L1, le bytecode des smart contracts est stocké sur la couche correspondante d’Ethereum et les transactions sont diffusées de pair-à-pair. Chaque nœud doit donc exécuter le bytecode avant de mettre à jour l’EVM.
Sur le L2, le bytecode est aussi stocké sur la couche dédiée du L1. Les transactions sont quant à elles diffusées hors-chaîne vers un nœud zkEVM. La zkEVM n’exécute pas le code : elle génère une preuve stipulant que l’état résultant des transactions est valide. C’est au niveau du L1 que le contrat vérificateur met à jour l’état de la blockchain, si la preuve est correcte, sans réexécuter les transactions.
Au niveau de l’EVM du L1 (exécution native), le bytecode est chargé dans la pile, puis tous les opcodes sont exécutés un par un. Chaque code opératif respecte ces trois étapes :
- Lecture des éléments de la pile, de la zone de mémoire ou de stockage ;
- Exécution des calculs ;
- Écriture des résultats dans la pile, en mémoire ou zone de stockage.
Les preuves de la zkEVM doivent donc s’assurer que le processus d’exécution respecte les conditions suivante:
- Le bytecode est correctement chargé à partir de la couche de stockage persistant ;
- Les opcodes sont exécutés un par un, de façon séquentielle, sans oubli ;
- Chaque opcode s’exécute correctement (il respecte les 3 étapes citées ci-dessus).
La zkEVM de Scroll est conçue autour de ces trois points fondamentaux.

Conception de la zkEVM de Scroll
Dans ce chapitre, nous allons plonger plus profondément dans les concepts qui donnent vie à la zkEVM. Ils permettent de traiter les trois aspects précédemment cités un par un.
L’accumulateur cryptographique
Un accumulateur est une primitive cryptographique permettant de justifier l’appartenance à un ensemble. Il fonctionne à sens unique, c’est-à-dire qu’il ne révèle pas les autres membres de l’ensemble.
Sur Scroll, on utilise un accumulateur pour prouver que la lecture de la zone de stockage persistant s’effectue correctement. En pratique, le bytecode déployé sur le L2 est stocké comme la feuille d’un arbre de Merkle. Le vérificateur peut alors s’assurer que le bytecode est correctement chargé à partir d’une adresse donnée. En effet, il lui suffit de vérifier le chemin correspondant dans l’arbre de Merkle : c’est une preuve succincte.
Tracer l’exécution des opcodes
Il faut pouvoir vérifier entièrement l’enchaînement des opérations, car le vérificateur ne connaît pas la destination des boucles conditionnelles ou des sauts présents dans le code.
La trace (le suivi) de l’exécution des opcodes peut être vue comme la version “décompressée” (“déroulée” si vous préférez) du bytecode. Il faut donc connaître tout les entrées (inputs) relatives au code exécuté.
Le prouveur fournit ainsi toutes les entrées du circuit, ainsi que le suivi de l’exécution des instructions. Ce tableau de suivi est aussi appelé “témoin” du circuit.
Prouver que l’exécution opcodes est correcte
On crée des circuits zkRollup pour chaque opcode de l’ensemble. Il faut ensuite prouver que la lecture, l’écriture et les opérations sont correctes.
Afin de ne pas faire exploser les frais, Scroll utilise deux techniques d’optimisation. Tout d’abord, on utilise deux preuves différentes pour la lecture/écriture et les calculs :
- Les éléments nécessaires aux opcodes sont regroupés dans un “bus” ou “State proof” (preuve d’état). Cette preuve assure que les opérations relatives à l’état, à la mémoire et à la pire sont correctes, mais vérifie pas que la lecture/écriture s’effectue au bon endroit.
- La deuxième preuve, ou “EVM Proof”, assure que les calculs opérés sur les éléments du “bus” sont corrects.
Cette séparation permet de générer la preuve des calculs sans prendre en compte l’intégralité de la zone de stockage d’Ehtereum.
Ensuite, chaque opcode est fragmenté, de façon spécifique, grâce aux polynômes, en fonction des besoins. Cela évite de surcharger le circuit de l’EVM à chaque étape.
C’est une architecture qui fut tout d’abord formalisée par la Fondation Ethereum. L’équipe de Scroll travaille activement à la développer : elle a ainsi implémenté plusieurs opcodes. Tous les travaux sont visibles sur GitHub.
L’architecture générale de Scroll
Scroll est composé de deux éléments principaux : la zkEVM et l’infrastructure du Layer 2 en elle-même. Le réseau des nœuds prouveurs est décentralisé, tandis que pour l’instant, le Séquenceur est centralisé.
Infrastructure du L2 de Scroll
L’infrastructure est faire de trois composants principaux :
- Les nœuds Scroll, qui permettent de créer les blocs du L2 à partir des transactions des utilisateurs. Ils assurent aussi la communication avec le L1 d’Ethereum.
- Le réseau des Rollers qui crée les preuves de validité pour la zkEVM.
- Les smart-contracts Rollup et Bridge, qui assurent la disponibilité des données pour les transactions ZK. Il jouent de plus le rôle de vérificateur pour les preuves, et permettent aux utilisateurs de transférer des actifs entre Ethereum et le L2.
Entrons dans le détail de chaque composant du système.
Les Scroll Nodes
Ces nœuds permettent aux utilisateurs et aux applications décentralisées d’interagir avec Scroll. Ils sont constitués de 3 modules.
Premièrement, le Séquenceur : il s’agit d’une interface JSON-RPC qui accepte les transactions du L2. Le Séquenceur pioche des transactions dans le mempool à intervalles réguliers (quelques secondes) pour former les blocs. À chaque bloc est associée une racine d’état. Le séquenceur est implémenté via Geth.
Deuxièmement, le Coordinateur : il reçoit le suivi de l’exécution du code une fois qu’un nouveau bloc est généré. Ce “témoin cryptographique” sera ensuite envoyé à un Roller, sélectionné aléatoirement.
Troisièmement, le Relayeur : il a accès aux contrats déployés sur Ethereum et Scroll (Bridge et Rollup). Il surveille le Rollup contract et donc le statut des blocs du L2 (disponibilité des données et preuves). De plus, le Relayeur assure la transmission des messages de transactions entre Ethereum et Scroll, via le Bridge.
Les Rollers
Les Rollers génèrent les preuves de validité des zkRollups : ils ont donc le rôle de prouveurs. Ces nœuds s’appuient sur l’accélération matérielle (GPU, ASIC, FPGA) pour réduire le délai de création des preuves et leurs coûts.
Génération d’une preuve de validité
Le schéma ci-dessous résume les différentes étapes du processus :

- Le Roller commence par convertir le suivi d’exécution venant du Coordinateur et crée le circuit des témoins.
- Il génère ensuite des preuves ZKP pour chaque circuit.
- Lors de l’étape finale, il agrège toutes les preuves des différents circuits du bloc en une seule.
Nous entrerons dans les détails de la génération des preuves plus loin dans l’article.
Les contrats Rollup et Bridge
Ce sont les deux contrats chargés d’assurer disponibilité des données et communication entre les deux layers, Ethereum et Scroll.
Le Rollup
Ce contrat reçoit les racines d’état et les blocs L2 de la part du Séquenceur.
Les racines d’état sont stockées sur Ethereum, tandis que les données des blocs L2 sont des calldata. C’est ce qui assure la disponibilité des données pour ces blocs, tout en profitant de la sécurité d’Ethereum. Le Relayeur peut ainsi toujours reconstruire les blocs.
Une fois que le contrat Rollup a vérifié la preuve de validité d’un bloc Scroll, il est considéré finalisé.
Le Bridge
De son côté, ce contrat permet aux utilisateurs d’échanger des messages entre le L1 et Scroll. De plus, il permet aux utilisateurs de bridger leurs ERC-20 entre Ethereum et Scroll, dans les deux directions. L’envoi de messages ou d’ERC-20 depuis Ethereum passe par une transaction sendMessage sur le Bridge. C’est ensuite le Relayeur qui indexe la transaction sur le L1, puis l’envoie au Séquenceur pour l’inclure dans un bloc du L2. Le même système est utilisé dans le sens inverse.
Fonctionnement des zkRollups de Scroll
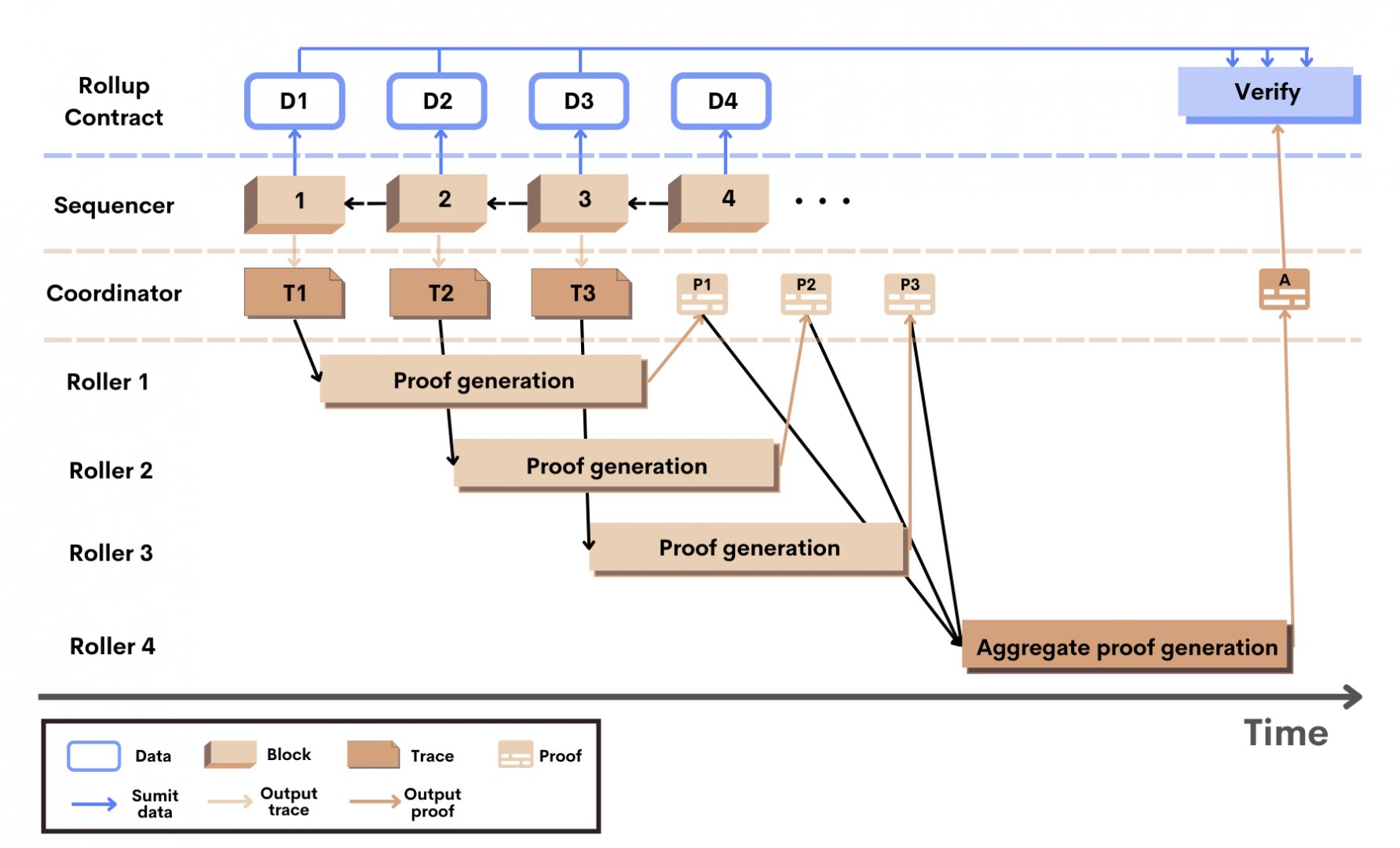
Le schéma ci-dessous résume la construction des zkRollups et des blocs du L2 avec Scroll. La finalisation des blocs du L2 sur la couche principale d’Ethereum n’intervient qu’après plusieurs étapes.
Construction des blocs sur Scroll
Tout d’abord, le Séquenceur va générer une séquence de blocs. Chaque bloc i présente également un suivi d’exécution T. Les blocs sont alors envoyés au Coordinateur. Dans le même temps, le Séquenceur va soumettre les données de transaction D au contrat Rollup sur Ethereum, ainsi que les racines d’état résultantes.
Ensuite, le Coordinateur sélectionne aléatoirement un Roller pour générer une preuve de validité pour les suivis d’exécution de chaque bloc. Il est possible de générer les preuves pour des blocs différents en parallèle, ce qui améliore le débit du système.
Après avoir généré la preuve P pour le bloc i, le Roller la renvoie au Coordinateur. Tous les k blocs, le Coordinateur va sélectionner un nouveau Roller, pour agréger les k preuves des blocs en une preuve globale A.
Enfin, le Coordinateur soumet la preuve agrégée A au contrat Rollup pour finaliser les blocs (i + 1 à i + k) du L2. Les preuves sont vérifiées grâce aux racines d’état et aux données de transaction, préalablement soumises au contrat.
Finalisation des blocs
La finalisation des blocs sur Ethereum comporte également plusieurs étapes. Chaque bloc passe par trois états :
- Precommited : le Séquenceur a proposé le bloc et l’a envoyé aux Rollers. le bloc n’est pas encore finalisé sur la chaîne du L2, mais les utilisateurs faisant confiance au séquenceur peuvent agir dessus par anticipation.
- Commited : le contrat Rollup a reçu les données de transaction du bloc. Pour l’instant, il n’y a pas de preuve que l’exécution est correcte.
- Finalized : le bloc est finalisé lorsque la preuve de validité de l’exécution de ses transactions est vérifiée on-chain sur Ethereum. Il fait alors partie de la chaîne canonique du L2 de Scroll.
La vérification des preuves via le L1 d’Ethereum confère donc le même niveau de sécurité pour la zkEVM de Scroll. Nous allons maintenant étudier comment sont construites les preuves de validité de Scroll.
Génération et coût des preuves sur Scroll
Les preuves à non-divulgation de connaissance (ZKP) sont un formidable outil ouvrant de nouvelles possibilités technologiques. Elles sont ainsi particulièrement utiles dans le domaine de la confidentialité (privacy) et de la scalabilité des blockchains. Cependant, la génération des ZKP n’est pas une mince affaire : elle est lente et coûteuse.
C’est donc le principal argument en défaveur des ZKP : afin de prouver l’exécution correcte d’un programme, il faut effectuer beaucoup plus de calculs que le programme lui-même. L’augmentation de la taille des calculs est de plusieurs ordres de grandeur.
Dans ce chapitre, nous allons décomposer la génération des preuves et donner une idée des coûts pour chaque étape.
Plonk
Il existe plusieurs systèmes de preuves (zk-SNARK) basés sur Plonk. Proposé en 2019, Plonk repose sur les permutations en bases de Lagrange. Depuis, ce système est largement adopté dans le domaine des ZKP, et plusieurs améliorations de Plonk ont vu le jour.
Scroll utilise ainsi une version modifiée d’Halo 2, le système de preuve basé sur Plonk conçu par l’équipe scientifique de ZCash. L’implémentation de Scroll intègre le schéma d’engagement polynômial KZG que nous décrirons plus bas.
Les polynômes
Les polynômes sont très utiles en cryptographie, car ils permettent de représenter des objets de grande taille, de façon simple et efficace. Dans le cas des ZKP, il s’agit de représenter un vecteur de dimension n (d’éléments appartenant à un corps fini).
Ce procédé s’appelle l’interpolation polynômiale :

Un polynôme peut être représenté de deux façons différentes :
- Sous forme du tuple de ses n coefficients : [p0, p1, …, pn−1] ;
- Sous forme du tuple de ses évaluations distinctes : [P(x0), P(x1), …, P(xn−1)] où les valeurs {x0, x1, …, xn−1} forment le domaine d’évaluation.
Le passage de la première représentation à la seconde est appelée transformation de Fourier, tandis que son inverse se nomme… la transformation de Fourier inverse.
Le calcul de ces transformations peut être effectué simplement. Dans le premier cas, il suffit de calculer le polynôme pour chaque xi du domaine d’évaluation. Dans le second, on utilise l’interpolation de Lagrange.
Ainsi, ces transformations peuvent être obtenues avec O(n²) calculs. Cependant, les polynômes des zkRollups sont de haut degré, il est donc préférable de trouver une méthode plus efficace : c’est le but de la transformation de Fourier rapide.
En algorithmique, la notation O() représente la limite supérieure du nombre d’itérations de l’algorithme, étant donnés n éléments en entrée.
La transformation de Fourier rapide
Cette amélioration de la transformation provient du fait que les ZKP manipulent des polynômes dans des corps finis (appelés aussi corps de Galois). Ainsi, cela restreint les coefficients et les points d’évaluation dans ce spectre. De plus, le domaine d’évaluation est également réduit (il devient un sous-groupe multiplicatif du corps fini).
Cette structure additionnelle rend la transformation plus efficace, grâce aux symétries mathématiques qu’elle engendre. Ainsi, nous passons de O(n²) opérations à O(n log n) pour la transformation de Fourier rapide et son inverse.
Le tableau de suivi
La « trace table » ou table de suivi est une matrice bidimensionnelle représentant le témoin ainsi que d’autres données utiles pour prouver qu’elle est correcte. Chaque cellule du tableau ci-dessous est est un élément appartenant à un corps fini.
Les colonnes A, B et C représentent les « données témoin » dites aussi « entrées privées« . Chaque ligne est une liste séquentielle de nombres de la suite de Square-Fibonnacci.
La i-ème ligne est donc le témoin pour le (i + 2)-ième nombre de Square-Fibonacci, puisque ce dernier utilise les deux valeurs précédentes pour le calculer.
La suite de Square-Fibonacci est une variation de la suite de Fibonacci classique :
– Soit f0 = 0, f1 = 1 ;
– Alors pour i ≥ 2, soit fi = (fi−2)²+(fi−1)² mod q, où q est un entier premier (très grand); le modulo limite la taille de chaque élément, pour qu’il puisse être représenté en une nombre fixé de bits.
La colonne S s’appelle le Sélecteur : elle indique qu’une relation mathématique particulière lie les éléments de la ligne. Un « 1 » indique que les trois premiers éléments de la ligne (a, b et c) doivent satisfaire c = a² + b² mod q. À l’inverse, un « 0 » indique que cette relation n’a pas à être satisfaire. La ligne vide au bas du tableau (ne comportant qu’un 0 pour la colonne S) est ajoutée pour rendre les calculs plus pratiques.
La colonne P correspond aux « entrées publiques« . Elle contient les entrées connues publiquement du circuit arithmétique.
Génération du témoin
Ce processus consiste à remplir le tableau de suivi. Il faut donc itérer sur chaque cellule du tableau, et trouver la valeur appropriée. L’arithmétique correspondante (dans des corps finis) est plus lourde que pour les types natifs (entiers et entiers longs). En effet, ces éléments nécessitent environ 256 bits pour être représentés, ce qui est supérieur à la taille des mots d’un CPU. Le fait de fragmenter les éléments ajoute un charge de calcul supplémentaire au calcul des valeurs mod q.
Dans l’exemple donnée par Scroll à travers la séquence de Square-Fibonacci, la charge de calcul est plus ou moins la même que pour le calcul originel. Cependant, pour des opérations plus complexes, la taille du tableau et la quantité d’opérations arithmétiques requises pour le remplir augmente considérablement.
Procédés additionnels
Une fois les données privées remplies, le tableau de suivi va subir un nouveau traitement. Les colonnes auxiliaires, également appelées « colonnes virtuelles« , servent à faciliter la vérification de la validité du tableau. Elles dépendent de certaines contraintes imposées par l’algorithme :
- Les wiring constraints (contraintes de câblage) : certaines cellules doivent avoir la même valeur. Dans le cas de la séquence de Square-Fibonacci, on doit donc avoir : ai+1 = bi et bi+1 = ci.
- Les tables de recherche du modèle Plonk.
Interprétation du tableau de suivi en polynômes
La colonne Z correspond à l’accumulateur polynômial, calculé à partir des données témoin. Il réduit la charge de calcul pour les contraintes imposées aux autres colonnes.
Cette colonne est donc un vecteur de dimension n composé d’éléments finis. Il représente la « forme d’évaluation » du polynôme de degré n – 1 : le i-ème élément de la colonne A correspond à la valeur du polynôme A(wi).
Calcul des engagements KZG
Une fois que les colonnes sont interprétées sous forme de polynômes, on peut procéder à la mise en gage. Le schéma d’engagement utilisé est ainsi le KZG (Kate-Zaverucha-Goldberg Polynomial Commitment Scheme).
Cela permet tout d’abord de compresser chaque colonne en une représentation plus courte : la taille de la table est donc fortement réduite.
De plus, l’utilisation d’un schéma d’engagement polynômial permet de générer des preuves d’évaluation. Elles servent à prouver qu’un polynôme passe bien par un point particulier sans avoir à révéler ce dernier.
Sans entrer dans les détails mathématiques du calcul des engagements KZG (voir la section « Ressources et bibliographie » pour de plus amples explications), voici quelques remarques :
- Le schéma nécessite un trusted setup (un nombre secret) ;
- On utilise les polynômes en base de Lagrange pour simplifier le calcul des engagements KZG à partir de la forme d’évaluation des polynômes.
Les calculs demandent de multiplier un vecteur de scalaires par un vecteur d’éléments de groupe. On appelle cela « multiplication multiscalaire« .
C’est une opération complexe (arithmétique de groupe). Ainsi, cette deuxième phase de la génération des preuves est plus lourde en calculs que le remplissage du tableau de suivi. Une simple addition au sein d’un groupe de courbes elliptiques demande un grand nombre d’opérations arithmétiques dans des corps finis.
Coûts de la phase KZG : une multiplication multiscalaire de taille n pour chaque colonne de longueur n.
Prouver que la table de suivi est correcte
Une fois la table de suivi remplie, et chaque colonne mise en gage via le schéma KZG la troisième phase débute : la vérification.
Afin d’être valide, le tableau de suivi original doit respecter une combinaison de contraintes. Dans l’exemple pris par Scroll, elles sont au nombre de 3 :
- La relation de Square-Fibonacci
- Les wiring constraints
- Les contraintes dues aux entrées publiques : la première ligne doit commencer par les deux premiers nombres de Square-Fibonacci, tandis que les cellules correspondant au n-ième nombre de Square-Fibonacci doivent correspondre au résultat avancé (inscrit dans la troisième ligne de la colonne P, les entrées publiques).
Toutes ces contraintes sont exprimées comme des relations entre les polynômes de la table. Les contraintes individuelles peuvent alors être linéairement combinées pour former une contrainte polynômiale unique (méta-contrainte). Cela provient du fait que les contraintes polynômiales individuelles doivent toutes être égales à zéro dans le domaine d’évaluation.
Cependant, plutôt que d’évaluer chaque polynômes pour tous les points du domaine, Scroll emploie une meilleure technique.
Le polynôme quotient
Il s’agit de dériver la proposition selon laquelle la contrainte polynômiale est valide pour chaque ligne du tableau de suivi. C’est équivalent à prouver qu’il existe un polynôme quotient respectant la propriété suivante :
Il existe un polynôme quotient Q(x) tel que ϕ(x)=Q(x)⋅(xn−1) où ϕ(x) est la méta-contrainte.
Le calcul du polynôme quotient est celui qui est le plus coûteux :
- Il faut convertir chaque polynôme d’une colonne de sa forme d’évaluation sous sa forme coefficient : O (n log n) en utilisant la transformation de Fourier rapide.
- Chaque polynôme nécessite ensuite 2n évaluations : 0 (2n log 2n) = 0 (n log n)
- Il faut ensuite, avec les 2n évaluations, calculer les 2n évaluations du polynôme quotient (arithmétique simple).
La mise en gage du polynôme quotient est effectuée de la même façon que les polynômes des colonnes. Cependant, le degré du polynôme quotient est bien plus élevé. Cela impliquerait donc d’utiliser une base de Lagrange spécifique, et donc un trusted setup différent (il doit être d’une taille supérieure au degré du polynôme quotient).
Scroll contourne ces calculs, en transformant le polynôme quotient en deux polynômes de degré inférieur à n. Il peut ainsi être engagé en utilisant une multiplication multi-scalaire de taille n. Cette opération requiert donc :
- Une transformation de Fourier rapide inverse de taille 2n ;
- 2 multiplications multiscalaires de taille n.
Prouver l’existence du polynôme quotient
Pour prouver l’existence du polynôme quotient, le vérificateur détient les éléments suivants :
- Les engagements KZG pour chaque colonne et pour le polynôme quotient ;
- Les preuves d’évaluation pour chaque colonne et pour le polynôme quotient au point α.
Il y a donc deux conditions à vérifier :
- La validité de chaque preuve d’évaluation ;
- La valeur correcte pour le polynôme quotient au point d’évaluation α.
Chaque preuve d’évaluation nécessite un appariement de courbes elliptiques, tandis que la vérification du polynôme quotient demande de l’arithmétique dans des champs finis. Au total, ces calculs nécessaires à la vérification des preuves sont beaucoup plus légers que ceux qui sont nécessaires à leur génération.
Améliorer la vitesse de Scroll
Il existe plusieurs axes d’amélioration pour accélérer la génération des preuves.
Accélération hardware
Les opérations complexes de type multiplication multiscalaire ou transformation de Fourier rapide représentent une part importante des calculs. Les CPU ne sont pas très rapides lorsqu’il s’agit d’exécuter les algorithmes associés. L’idée est donc plutôt d’utiliser des GPU, ASIC ou FPGA : la recherche d’algorithmes adaptés est foisonnante.
Réduction du nombre de colonnes dans la table
Il s’agit de trouver de nouvelles techniques de calcul, de façon à alléger le tableau de suivi. C’est également un domaine de recherche qui peut améliorer grandement l’efficacité du système.
Parallélisation
Certaines tâches nécessaires à la génération des preuves sont parallélisables, comme les schémas d’engagement polynomial des colonnes. De plus, le schéma d’engagement (basé sur la multiplication multiscalaire) pour chaque colonne témoin peut être calculé en même temps que sa génération. Cela permet d’augmenter la vitesse globale du schéma de génération des preuves de validité de façon substantielle.
Systèmes de preuves alternatifs
La recherche théorique dans le domaine des ZKP est très active. Il existe de nombreux systèmes de preuve : chacun présente un certain coût en calculs. À l’avenir, les scientifiques pourraient concevoir des systèmes plus performants.
Utiliser Scroll et participer à son développement
Si Ethereum et ses solutions de couche secondaire piquent votre curiosité, n’hésitez pas à tester Scroll ! Le testnet est déjà disponible en version alpha.
La version pré-alpha du testnet fut lancée en août 2022. On peut parler de succès, puisque la communauté regroupe plus de 100 000 utilisateurs. Plus de 15 400 000 transactions ont été effectuées sur ce testnet et 1 800 000 blocs ont été prouvés. Plus de 641 000 batches ont été soumis comme preuves de validité, et finalisés par le contrat Rollup de Scroll sur le L1.
La version alpha du testnet de Scroll est accessible sur Goerli (l’un des réseaux de test d’Ethereum). Afin d’y participer, il faut suivre les quelques étapes mentionnées sur le portail dédié :
Bien entendu, il faut disposer d’un wallet (comme MetaMask) correctement configuré. Il faut en premier lieu importer la chain ID et les URL des RPC pour le Testnet en cliquant les boutons “Add to wallet” de la page. Le testnet Goerli est configuré par défaut sur MetaMask.
Pour utiliser d’autres wallets, et configurer manuellement le chain ID et le RPC, toutes les informations sont disponibles dans la documentation dédiée.
Rejoindre l’équipe de développement
Afin de participer au développement de cet ambitieux projet, d’aucuns peut entrer en contact avec la Core Team sur Discord, par exemple (tous les liens utiles sont présents à la fin de l’article). Bien entendu, il faut un bagage technique conséquent. Voici les profils recherchés :
- Chercheurs dans le domaine des ZKP ;
- Développeurs ZKP, Golang ou Solidity ;
- Ingénieurs GPU ;
- Animateurs de communauté.
Ressources et bibliographie
Voici tous les liens pouvant être utiles pour utiliser Scroll ou approfondir sa connaissance d’Ethereum, de l’EVM, des ZKP et des mathématiques sous-jacentes.
Scroll
Ethereum et ZKP
- The Keccak Reference – Guido Bertoni, Joan Daemen, Michaël Peeters, Gilles Van Assche
- Merkle Patricia Trie – Documentation d’Ethereum
- Référence des opcodes de l’EVM
- Exploring Elliptic Curve Pairings – Vitalik Buterin
zkRollups et Mathématiques
- An Incomplete Guide to Rollups – Vitalik Buterin
- Rank-1 Constraint System with Application to Bulletproofs – TariLabs (spécifications du R1CS, circuits arithmétiques)
- Scalable Zero Knowledge via Cycles of Elliptic Curves – Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, Madars Virza
- SNARKs for C: Verifying Program Executions Succinctly and in Zero Knowledge – Eli Ben-Sasson, Alessandro Chiesa, Daniel Genkin, Eran Tromer, Madars Virza (comprendre TinyRAM)
- Optimising Halo and Constructing Graphs of Elliptic Curves – Daira Hopwood
- POSEIDON: A New Hash Function for Zero-Knowledge Proof Systems – Lorenzo Grassi, Dmitry Khovratovich, Christian Rechberger, Arnab Roy, Markus Schofnegger
- Cairo : a Turing-complete STARK-friendly CPU architecture – Lior Goldberg, Shahar Papini, and Michael Riabzev
- Aztec emulated field and group operations – Ariel Gabizon (comprendre Aztec)
- KZG polynomial commitments – Dankrad Feist
- Understanding PLONK – Vitalik Buterin (introduction à Plonk)
- PlonK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge – Ariel Gabizon, Zachary J. Williamson, Oana Ciobotaru (le livre blanc complet de Plonk)
- Explaining Halo 2 – Sean Bowe
- Inner Product Arguments – Dankrad Feist (le modèle utilisé sur la version de base d’Halo 2 via l’engagement de Pedersen)
- Le code source d’Halo 2
- La version modifiée incluant le schéma d’engagement KZG
- PCS multiproofs using random evaluation – Dankrad Feist (comprendre le calcul des engagements KZG)
- STARK 101 – Excellent tutoriel de Starkware sur les ZKP avec l’exemple de la suite de Square-Fibonacci
- From AIRs to RAPs – how PLONK-style arithmetization works – Ariel Gabizon (comprendre l’arithmétisation)
- Multiset checks in PLONK and Plookup – Ariel Gabizon (comprendre la vérification des contraintes de Plonk)
- Kate-Zaverucha-Goldberg (KZG) Constant-Sized Polynomial Commitments – Alin Tomescu (comprendre la génération des preuves d’évaluation KZG)
Pour conserver vos cryptos, rien ne vaut un wallet Ledger. Les Nano S et Nano X procurent sécurité et facilité d’utilisation. En effet, ils sont compatibles avec l’immense majorité des cryptos et des réseaux. Ils constituent une alternative absolument essentielle à tous les exchanges qui proposent de conserver vos avoirs à votre place. Rappelez-vous, “Not your keys, not your coins” (lien commercial) !