30 Février 2023, 12h00 CET — La nouvelle se répand comme une traînée de poudre. Les threads se multiplient sur Twitter pour présenter les preuves on-chain des événements de la nuit. Les crypto-experts sont unanimes et ne présentent aucun doute. Le wallet de Satoshi Nakamoto est vide.
Plus alarmant encore, il n’est pas le seul. D’autres mouvements viennent d’être détectés sur des wallets de l’ère Satoshi. Notamment un certain portefeuille appartenant au feu cypherpunk Hal Finney, connu pour avoir reçu la première transaction en bitcoin de l’histoire. La panique s’empare du marché, la volatilité du Bitcoin explose et les exchanges affichent 14 000 $. Les internautes commencent à envisager le pire. Si le wallet de notre regretté Hal Finney a, lui aussi, été vidé, il ne peut y avoir que deux explications. Soit Nakamoto avait accès à sa clé privée. Soit, nous assistons à un événement d’une envergure sans précédent, n’annonçant pas seulement la mort de Bitcoin.
Table des matières
Dans mon précédent article, je vous ai présenté le principe de la signature électronique et les conditions élémentaires auxquelles elle doit répondre pour permettre votre authentification sur la blockchain ainsi que l’échange de clé Diffie-Hellman posant les bases de la cryptographie asymétrique. Aujourd’hui, nous allons plonger dans le premier protocole cryptographique permettant des signatures électroniques robustes, le chiffrement RSA.
Mais avant cela, rappelez-vous, je vous ai donné un léger sursis sur les mathématiques modulaires. « Cette fois, vous n’y échapperez pas » – lâchais-je d’une voix machiavélique derrière mon clavier. Mais soyez sans crainte, c’est plutôt simple à comprendre, vous en faites tous les jours sans le savoir !
Horlogerie et mathématiques modulaires
Oubliez tout ce que vous savez, dorénavant, 12 = 0
La semaine dernière, je vous ais donc parlé des mathématiques modulaires qui servaient, dans l’échange de clé Diffie-Hellman, à simplifier les calculs que doivent faire nos deux interlocuteurs Alice et Bob. Cependant, son implication dans le chiffrement RSA est bien plus importante, car elle intervient directement dans le chiffrement et le déchiffrement des messages entre nos deux intervenants, c’est pourquoi je vais tenter de vous l’expliquer.
Que se passerait-il si nous découvrions que 12 ≡ 0 ?
(J’utilise ici le signe triple égal par rigueur mathématique. Eh oui, ce n’est pas le symbole d’Ethereum bien qu’il soit très proche, comprenez ici simplement 12 = 0. Le signe triple égal sera utilisé dès que nous parlerons d’une égalité dans un système modulaire).
Spoiler, ceci bouleverserait notre manière de calculer, mais vous en faites déjà l’expérience tous les jours !
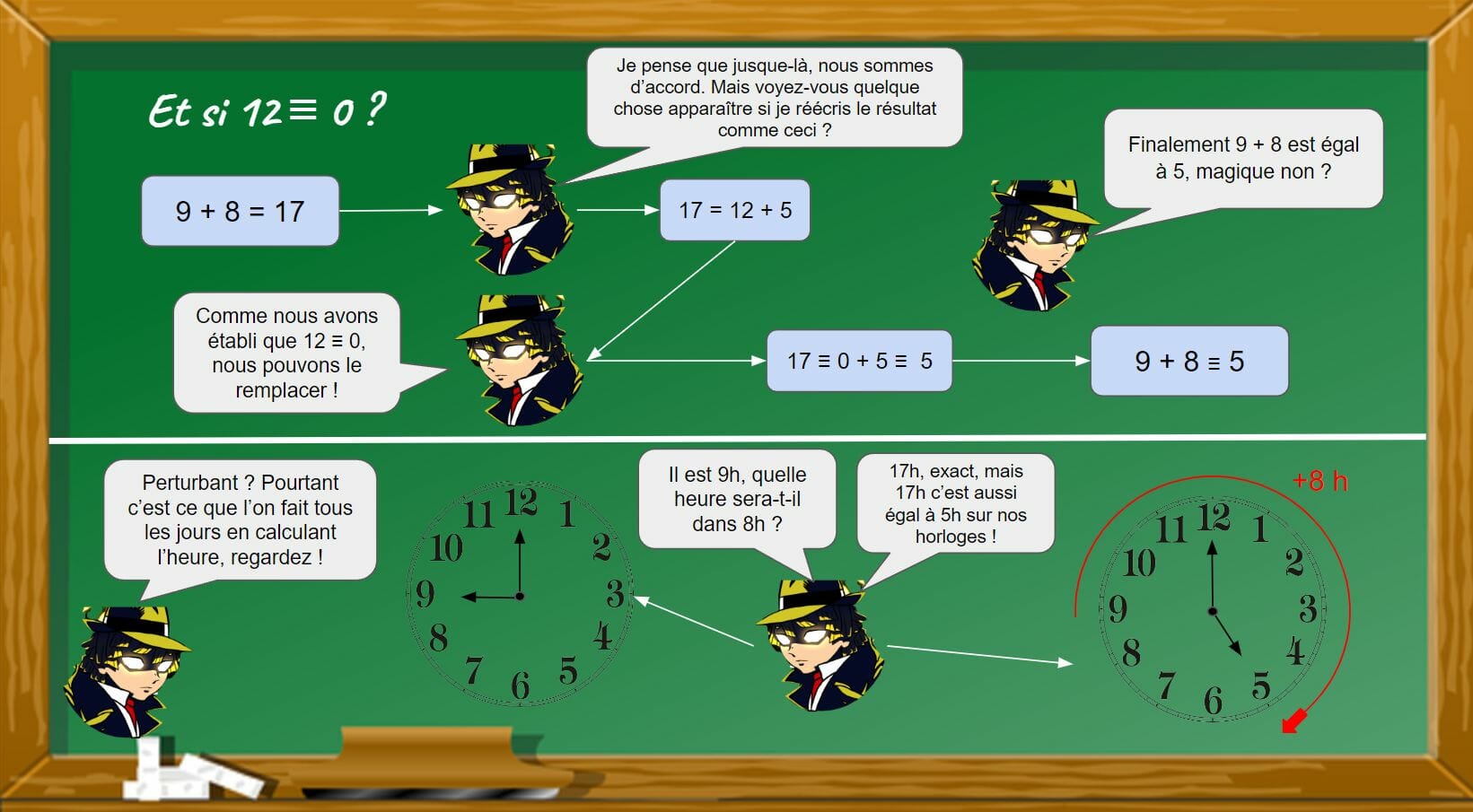
Pour les plus matheux d’entre vous, cela devrait vous rappeler le cercle trigonométrique. Sur ce cercle 2π est égale à 0, de même pour 4π, 6π, etc. Il en est de même pour nos horloges, 17h est aussi égal à 5h. La mathématique modulaire revient enrouler la droite de tous les nombres autour d’un cercle selon un cycle prédéfini. 12 dans l’exemple de nos horloges. On dit que nous sommes dans une mathématique modulo 12.
Quels avantages pour la cryptographie ?
« Ok Foudres, c’est très bien, mais quelle application dans la cryptographie ? Je ne vois toujours pas le rapport » me direz-vous.
Patience, j’y viens ! Dans l’échange de clé Diffie-Hellman, nous réalisions des calculs avec des puissances de nombre gigantesque, voici ce qu’il se passe lorsque nous appliquons une mathématique modulo 12.
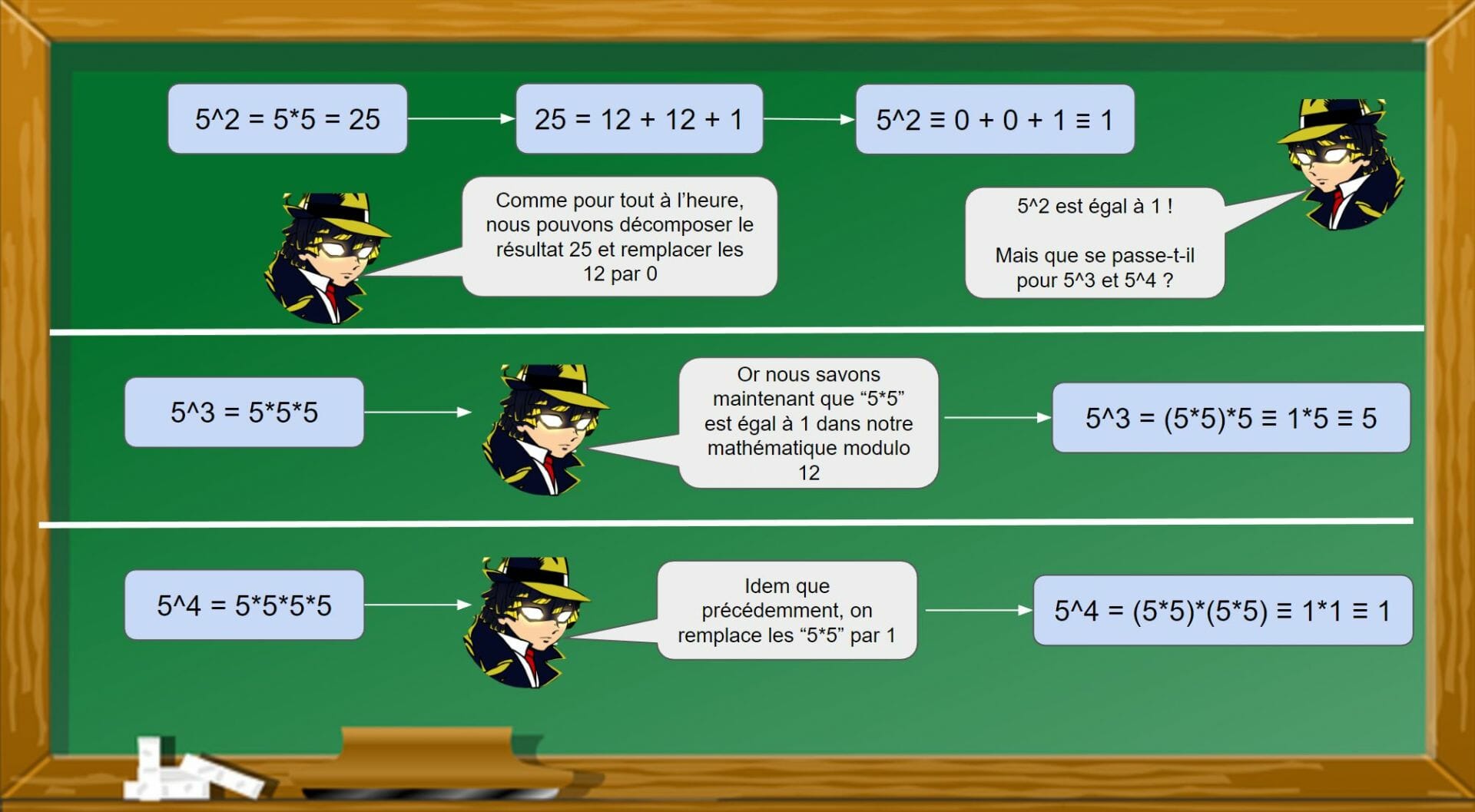
Voyez-vous ce que cela va induire ? La mathématique modulo 12 nous permet de simplifier 5^2 par 1. À partir de ce calcul, nous pouvons simplifier n’importe quelle puissance de 5 :
- Pour toute puissance paire : 5^(nombre pair) sera égale à 1,
- Pour toute puissance impaire : 5^(nombre impair) sera égale à 5.
C’est ce petit tour de passe-passe mathématique qui permet d’utiliser les fonctions de puissance avec des nombres cryptographiquement grands. Petit test pour vérifier si vous avez compris la logique :
Dans une mathématique modulo 12, quel est le résultat de 5^974896232 ?
Nous écrirons le résultat comme ceci : 5^974896232 ≡ 1 (mod 12) — avec mod pour modulo.
Facile non ? (oui, j’essaye totalement de me convaincre que mes explications ont été claires.) Maintenant que les mathématiques modulaires ne sont plus un mot barbare pour vous, nous allons pouvoir passer au chiffrement RSA. Accrochez-vous, car cela sera la partie la plus complexe de ma série sur la cryptographie !
Chiffrement RSA
La construction des clés publique et privée
Le chiffrement RSA tiré du nom des initiales de ses trois inventeurs, Ronald Rivest, Adi Shamir et Leonard Adleman, utilise la cryptographie asymétrique en se basant sur les travaux de Diffie-Hellman. Là où l’échange de clé Diffie-Hellman ne permet que la création d’une clé de chiffrement sans accord non chiffré au préalable, le protocole RSA va plus loin en permettant directement l’échange d’informations via le chiffrement à clé publique. Le protocole RSA introduit les fonctions à trappe.
Elles possèdent les mêmes propriétés que les fonctions à sens unique expliquées dans mon précédent article, hormis le fait qu’elles possèdent ce qu’on appelle une « backdoor », un nombre permettant la réversibilité de la fonction de chiffrage.
Alice et Bob, toujours eux, veulent échanger et signer un document et n’ont jamais interagi par le passé. Alice va créer une paire de clés, une clé privée qui servira à Alice pour signer le document de Bob, et une clé publique, qui servira à vérifier que la signature provient bien d’Alice.
(D’avance, ne vous encombrez pas trop avec les détails mathématiques en rouge si vous peinez à les comprendre. Retenez simplement la logique).

Alice a donc trois nombres en sa possession. Le nombre public N, sa clé publique d et sa clé privée e. Ces derniers sont tous calculés grâce aux nombres p et q qu’elle doit absolument détruire afin de ne pas compromettre sa clé privée !
Comment transformer des mathématiques en signature électronique
C’est ici que la mathématique modulaire expliquée plus haut va opérer sa magie :

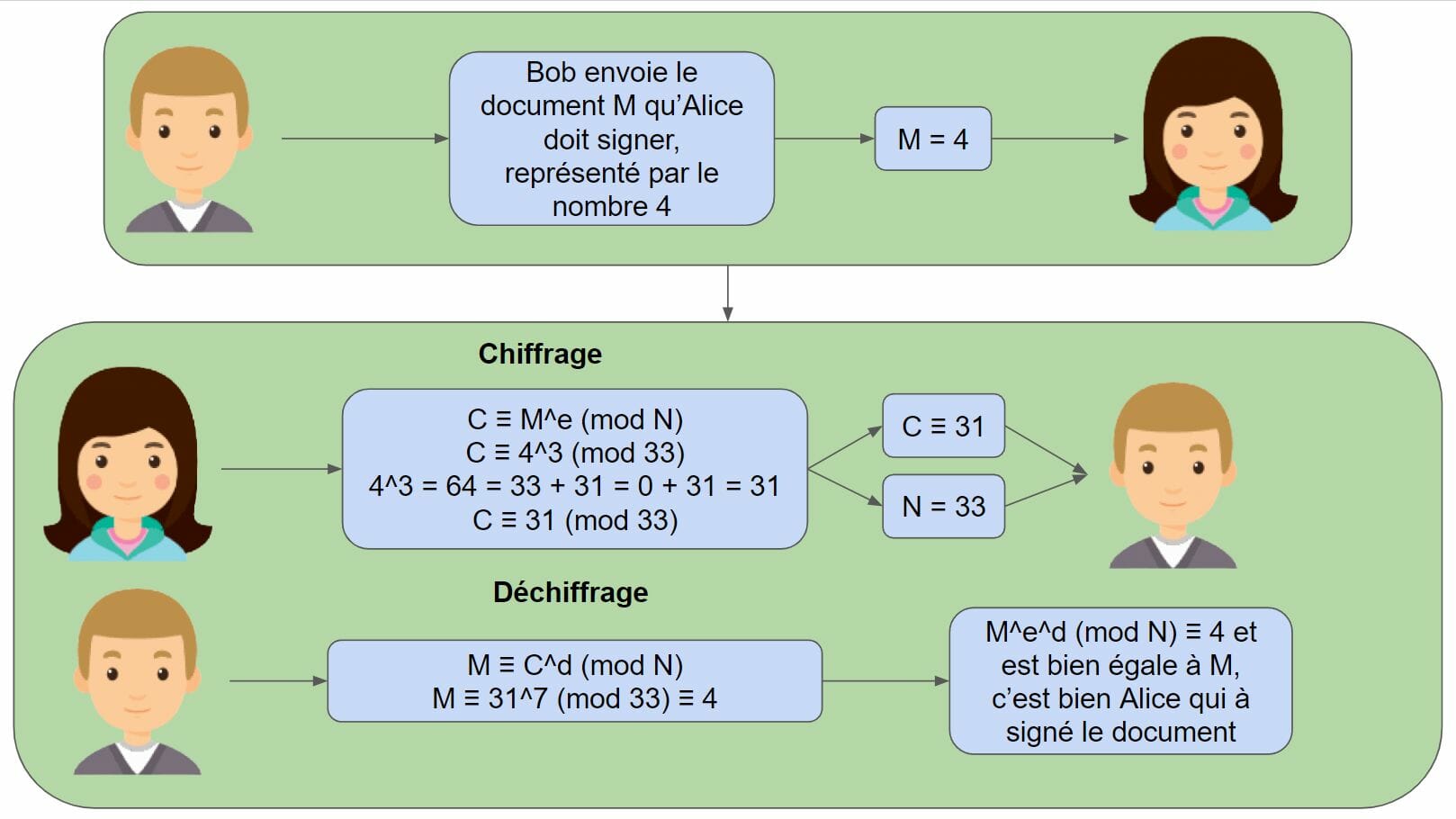
- Bob veut faire signer un document M à Alice.
- Alice réalise le calcul : C = M^e mod N et envoie le résultat C, qui représente sa signature, et le nombre N à Bob.
- Bob réalise le calcul : C^d (mod N) soit M^e^d (mod N). Si grâce à ce calcul Bob retrouve bien le document M tel qu’il l’a envoyé à Alice. C’est qu’Alice l’a bien signé avec sa clé privée.
Grâce à notre mathématique modulaire, nous avons donc en résumé, un chiffrage par la clé privée d’Alice et un déchiffrage par sa clé publique :
(Document) ^ (Clé privée d’Alice) ^ (Clé publique d’Alice) = Document
Si vous vous souvenez de la propriété des « fonctions puissance » présentées la dernière fois, l’inverse est totalement possible. Bob peut envoyer un message chiffré à Alice à l’aide de sa clé publique qu’elle seule saura déchiffré. Mais ce n’est pas équivalent, car rien ne permettra à Alice d’être sûre que c’est Bob qui lui a envoyé le message chiffré, puisqu’il l’est avec sa clé publique. C’est ce que l’on appelle l’attaque du “man-in-the-middle”.
Pour répondre à ce problème, Bob devra lui aussi signer le message avec sa propre clé privée avant de le chiffrer avec la clé publique d’Alice. Ensuite, Alice sera en mesure d’en vérifier la provenance avec la clé publique de Bob, et le déchiffrer avec sa clé privée.
Robustesse et propriété du chiffrement RSA
La robustesse de ce chiffrement vient de l’impossibilité pour une tierce personne de retrouver la clé privée d’Alice seulement grâce aux nombres publiques N, C et d dans un temps raisonnable. Ceci vient de la complexité, et du temps de calcul déraisonnablement long, nécessaire pour réaliser la décomposition en facteur premier du nombre public N afin de retrouver p et q. Nombre qui permettraient de retrouver facilement par brute force la clé privée d’Alice.
Aujourd’hui, nous savons trouver cette décomposition par « brute force » avec des nombres de 795 bits. Mais les clés RSA couramment utilisées sont de 2048 bits, ce qui nous laisse encore un peu de marge. Cependant, quelques doutes planent à cause d’un algorithme quantique pouvant casser RSA relativement facilement, l’algorithme de Shor.
Pour revenir à la signature électronique, ici, Bob met au défi Alice de signer le document M avec sa clé privée, si ce dernier ne retrouve pas le document M à l’identique via la vérification grâce à la clé publique d’Alice. C’est que ce n’est pas Alice qui a signé le document ! La signature répond donc bien à tous les critères mentionnés dans le précédent article, à savoir :
Authenticité : Alice est authentifiée par sa clé privée qu’elle seule possède.
Infalsifiabilité : la clé privée d’Alice est mathématiquement infalsifiable, car protégée par l’impossibilité de réaliser une décomposition en facteur premier.
Non-réutilisabilité : la signature C est unique, car dérivée du document et de la clé privée d’Alice.
Inaltérabilité : la signature C sert de preuve comme elle est dérivée du document lui-même. Si le document est modifié, Alice n’aura qu’à le signer à nouveau et montrer que sa signature est différente de la précédente.
Irrévocabilité : Les règles ci-dessus étant respectées, Alice ne peut pas démentir sa signature.
Assez de formules alambiquées pour aujourd’hui, je sens vos yeux s’alourdir après toutes ces pirouettes mathématiques. La prochaine fois, nous irons creuser Bitcoin et le big boss des protocoles de chiffrement, le protocole ECDSA, puis nous finirons sur le hashage et son rôle dans la preuve de travail !
30 Février 2023, 16h00 CET Les mains moites, la sueur au front, les experts en cryptographie déploient tous leurs efforts pour essayer d’éclaircir la situation. Ils repassent en revue tous les concepts mathématiques et protocoles de cryptographie à la recherche d’une faille, d’un détail, qui serait passé inaperçu pendant plus de cinquante ans. Alors que la réponse doit se cacher là, sous leurs yeux, l’incompréhension pousse les accusations à se faire de plus en plus grandissantes envers Google et la Chine, accablés d’avoir utilisé leur ordinateur quantique afin d’envoyer Bitcoin outre-tombe. L’étau se resserre, mais cette énigme reste, pour l’instant, encore insondable. Sa résolution n’est malheureusement pas encore à la portée de notre compréhension.
En crypto, ne faites pas l’économie de la prudence ! Ainsi, pour conserver vos avoirs cryptographiques à l’abri, la meilleure solution est encore un wallet hardware personnel. Chez Ledger, il y en a pour tous les profils et toutes les cryptos. N’attendez pas pour mettre vos capitaux en sécurité (lien commercial) !